Samacheer Kalvi 10th Maths Guide Chapter 1 உறவுகளும் சார்புகளும் Ex 1.3

Tamilnadu State Board New Syllabus Samacheer Kalvi 10th Maths Guide Pdf Chapter 1 உறவுகளும் சார்புகளும் Ex 1.3 Textbook Questions and Answers, Notes.

TN Board 10th Maths Solutions Chapter 1 உறவுகளும் சார்புகளும் Ex 1.3

கேள்வி 1.
f = { (x,y)/x, y ∈ N மற்றும் y = 2x } ஆனது N-ன் மீதான ஒரு உறவு என்க. மதிப்பகம், துணை மதிப்பகம் மற்றும் வீச்சகத்தைக் காண்க. இந்த உறவு சார்பாகுமா?
தீர்வு :
x, y ∈N
x = {1,2,3 ……}
y = {1,2,3….}
கணக்கின்படி y = 2x
x = 1 எனில் y = 2 x 1 = 2
x = 2 எனில் y = 2 x 2 = 4
x = 3 எனில் y = 2 x 3 = 6
∴ R = {(1,2), (2,4), (3,6), …….)
மதிப்பகம் = {1, 2, 3, ……………….}
துணை மதிப்பகம் = {1, 2, 3, 4……….}
சார்பகம் = {2, 4, 6, ………………}
இந்த உறவு சார்பு ஆகும்.

கேள்வி 2.
x = {3, 4, 6, 8) என்க . R ={(x, f(x) | x ∈ X, f(x) = x² + 1} என்ற உறவானது X- லிருந்து N க்கு ஒரு சார்பாகுமா?
தீர்வு :
தரவு f(x) = x² + 1 இங்கே X = {3, 4, 6, 8}
f(3) = 3² + 1 = 9 + 1 = 10
f(4) = 4² + 1 = 16 + 1 = 17
f(6) = 6² + 1 = 36 + 1 = 37
f(8) = 8² + 1 = 64 + 1 = 65
இது ஒரு சார்பு ஆகும்
காரணம் : Xல் உள்ள ஒவ்வொரு உறுப்பிற்கும்
N ல் ஒரே ஒரு உறுப்புடன் தொடர்புள்ளது.

கேள்வி 3.
கொடுக்கப்பட்ட சார்பு f 😡 → x² – 5x + 6, எனில்
(i) f(-1)
(ii) f(2a)
(iii) f(2)
(iv) f(x-1)
ஆகியவற்றை மதிப்பிடுக.
தீர்வு :
f(x) = x² – 5x + 6)
i) x = -1 எனில்
f(-1) = (-1)² – 5(-1) + 6
= 1 + 5 + 6
= 12

ii) x = 2a எனில்
f(2a) = (2a)² – 5(2a) = 6
= 4a² -10a + 6

iii) x = 2 எனில்
f(2) = (2)² – 5(2) + 6 = 4-10+6
= 0

iv) x = x-1 எனில்
f(x-1) = (x-1)² – 5(x-1) + 6
= x² – 2x + 1 -5x + 5 + 6
= x² – 7x + 12

கேள்வி 4.
படம் 1.16 ல் கொடுக்கப்பட்ட வரைபடம் f(x) யின் மூலமாக f(9) = 2 என்பது தெளிவாகிறது.

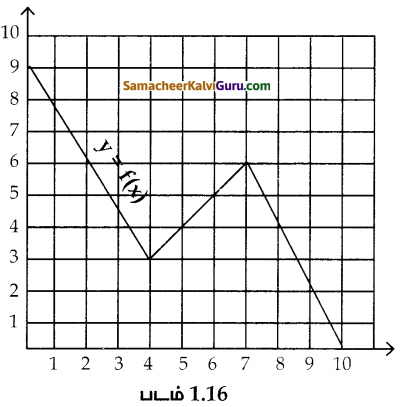
i) பின்வரும் சார்புகளின் மதிப்புகளைக் காண்க.
(அ) f (0) (ஆ) f (7) (இ) f (2) (ஈ) f (10)
ii) x-இன் எம்மதிப்பிற்கு f(x) = 1 ஆக இருக்கும்?
iii) படம் 1.16 யில் (i) மதிப்பகம் (ii) வீச்சகம் காண்க.
iv) f என்ற சார்பில் 6 -ன் நிழல் உரு என்ன?
தீர்வு :
i) (a) f (0) = 9)
(b) f (7) = 6
(c) f (2) = 6
(d) f (10) = 0

ii) f (x) = 1 எனில் x ன் மதிப்பு 9.5
iii) மதிப்பகம் = {0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10}
வீச்சகம் = {0, 1, 2, 3, 4, 5, 6, 7, 8, 9}
iv) 6ன் நிழல் உரு 5

கேள்வி 5.
f(x) = 2x + 5 என்க. x ≠ 0 எனில், \(\frac{f(x+2)-f(2)}{x}\) ஐக் காண்க.
தீர்வு :
தரவு f(x) = 2x + 5
f(x + 2) = 2(x+2) + 5
= 2x + 4 + 5
= 2x +9

f(2) = 2(2) + 5
= 4 + 5 = 9
\(\frac{f(x+2)-f(2)}{x}=\frac{2 x+9-9}{x}=\frac{2 x}{x}\) = 2

கேள்வி 6.
ஒரு சார்பு f ஆனது f(x) = 2x – 3 என வரையறுக்கப்பட்டால்
i) \(\frac{f(0)+f(1)}{2}\) ஐக் காண்க
ii) f(x) = 0 எனில், x – ஐக் காண்க
iii) f(x) = x எனில், x – ஐக் காண்க
iv) f(x) = f(1-x) எனில், x – ஐக் காண்க
தீர்வு :
தரவு f(x) = 2x – 3 எனில்
f(0) = 2(0) – 3 = 0 – 3 = -3
f(1) = 2(1) – 3 = 2 – 3 = -1
(i) \(\frac{\mathrm{f}(0)+\mathrm{f}(1)}{2}=\frac{-3-1}{2}=\frac{-4}{2}\) = -2
ii) தரவு f(x) = 0 எனில்
2x – 3 = 0
2x = 3 ⇒ x = \(\frac{3}{2}\)

iii) தரவு f(x) = x எனில்
2x – 3 = x
2x – x = 3
x = 3

iv) தரவு f(x) = f(1-x) எனில்
2x – 3= 2(1-x) -3
2x – 3 = 2 – 2x -3
2x – 3 = -1 – 2x
2x + 2x = -1 +3
4x = 2 ⇒ x = \(\frac{2}{4}=\frac{1}{2}\)

கேள்வி 7.
24 செ.மீ பக்க அளவுள்ள சதுர வடிவத் துண்டிலிருந்து நான்கு மூலைகளிலும் சம அளவுள்ள சதுரங்களை வெட்டிப்படம் 1.17 ல் உள்ளவாறு மேல் புறம் திறந்த ஒரு பெட்டி செய்யப்படுகிறது. இந்தப் பெட்டியின் கன அளவு Vஎனில், V ஐx -யின் சார்பாகக் குறிப்பிடுக.

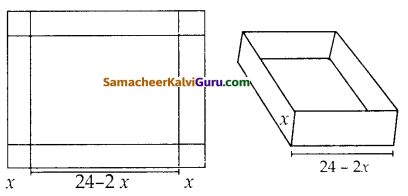
தீர்வு :
நீளம் = 24 – 2x
அகலம் = 24 – 2x
உயரம் = x
பெட்டியின் கன அளவு = l x b x h
= (24 – 2x) x (24 – 2x) x x
= (24 – 2x)² x x
= (576 – 96x + 4x²) x x
= 4x³ – 96x² + 576x

கேள்வி 8.
f என்ற சார்பு f(x) = 3 – 2x என வரையறுக்கப்படுகிறது. f(x²) = (f(x))² எனில் Xஐக் காண்க.
தீர்வு :
f(x) = 3 – 21 எனில்
f(x) = 3 – 2x²
[f(x)]? = (3 – 23)²
கணக்கின் படி f(x2) = [f(x)]²
3 – 2x² = (3 – 2x)² |
3 – 2x² = 9 – 12x + 4x²
4x² + 2x² – 12x = 3 – 9
6x² – 12x = -6
6x² – 12x + 6 = 0
÷6 ⇒ x² – 2x + 1 = 0
⇒ (x – 1)² = 0
⇒ x- 1 = 0
∴ x = 1

கேள்வி 9.
ஒரு விமானம் 500 கி.மீ / மணி வேகத்தில் பறக்கிறது. விமானம் ‘d’ தொலைவு செல்வதற்கு ஆகும் காலத்தை f (மணியில்)-ன் சார்பாக வெளிப்படுத்துக.
தீர்வு :
வேகம் = 500 கி.மீ / மணி
காலம் = t நேரம் என்க
தூரம் = வேகம் X நேரம்
= 500 x t = 500 t

கேள்வி 10.
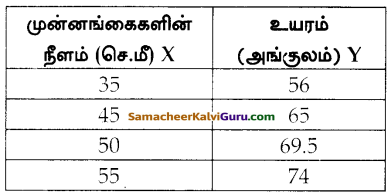
அருகில் உள்ள அட்டவணையில் நான்கு நபர்களின் முன்னங்கைகளின் நீளம் மற்றும் அவர்களுடைய உயரங்களின் தகவல்கள் வழங்கப்பட்டுள்ளன. அந்த விவரங்களின் அடிப்படையில் ஒரு மாணவர், உயரம் (y) மற்றும் முன்னங்கை நீளம் (x)-க்கான உறவை y = ax + b எனக் கண்டுபிடித்தார். இங்கு a மற்றும் b ஆகியவை மாறிலிகள்.
i) இந்த உறவானது சார்பாகுமா என ஆராய்க.
ii) a மற்றும் b – ஐக் காண்க.
iii) முன்ன ங்கையின் நீளம் 40 செ.மீ எனில், அந்த நபரின் உயரத்தைக் காண்க.
iv) உயரம் 53.3 அங்குலம் எனில், அந்த நபரின் முன்னங்கையின் நீளத்தைக் காண்க

தீர்வு :
உறவு V = 0.9.x + 24.5 ஆகும்
i) இது ஒரு சார்பு
ii) y = ax + b உடன் ஒப்பிடுகையில்
a = 0.9, b = 24.5
iii) முன்னங்கையின் நீளம் 40 செ.மீ எனில் பெண்ணின் உயரம் 60.5 அங்குலம் ஆகும்.
y = (0.9 x 40 + 24.5
= 36 + 24.5
= 60.5
iv) உயரம் 53.3 அங்குலம் எனில் பெண்ணின் முன்னங்கையின் நீளம் 32 செ.மீ
53.3 = 0.9x + 24.5
∴ x = 32