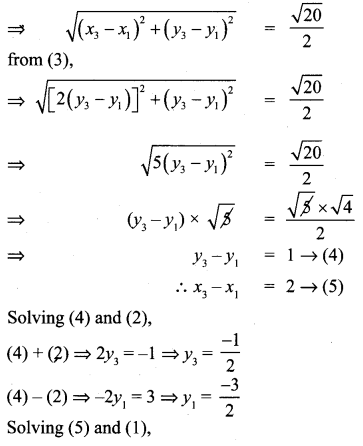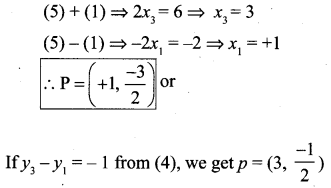You can Download Samacheer Kalvi 10th Maths Book Solutions Guide Pdf, Tamilnadu State Board help you to revise the complete Syllabus and score more marks in your examinations.
Tamilnadu Samacheer Kalvi 10th Maths Solutions Chapter 5 Coordinate Geometry Ex 5.2
10th Maths Exercise 5.2 Samacheer Kalvi Question 1.
What is the slope of a line whose inclination with positive direction of x -axis is
(i) 90°
(ii) 0°
Solution:
(i) θ = 90°
m = tan θ = tan 90° = ∝ (undefined)
(ii) m = tan θ = tan 0° = 0
Exercise 5.2 Class 10 Samacheer Kalvi Question 2.
What is the inclination of a line whose slope is (i) 0
Solution:
(i) Slope = 0
tan θ = 0
tan 0 = 0
∴ θ = 0°
(ii) Slope = 1
tan θ = 1
tan 45° = 1
∴ θ = 45°
angle of inclination is 45°
Ex 5.2 Class 10 Samacheer Question 3.
Find the slope of a line joining the points
(i) (5, \(\sqrt{5})\)) with origin
(ii) (sin θ, -cos θ) and (-sin θ, cos θ)
(i) (5, \(\sqrt{5})\)) with origin (0, 0)
Solution:
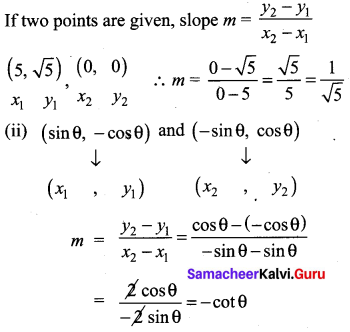
10th Maths Exercise 5.2 Question 4.
What is the slope of a line perpendicular to the line joining A(5, 1) and P where P is the mid-point of the segment joining (4, 2) and (-6,4).
Solution:
P is the mid point of the segment joining (4, 2) and (-6, 4)

10th Maths Ex 5.2 Question 5.
Show that the given points are collinear (-3, -4), (7, 2) and (12, 5)
Solution:
The verticles are A(-3, -4), B(7, 2) and C (12, 5)
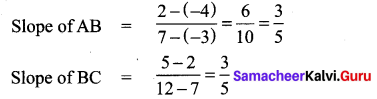
Slope of AB = Slope of BC
∴ The points A, B and C lie on the same line.
∴ They are collinear.
10th Maths Exercise 5.2 Solution Question 6.
If the three points (3, -1), (a, 3), (1, -3) are collinear, find the value of a.
Solution:
Slope of AB = slope of BC.

Samacheer 10th Maths Exercise 5.2 Solutions Question 7.
The line through the points (-2, a) and (9, 3) has slope –\(\frac{1}{2}\). Find the value of a.
Solution:
A line joining the points (-2, a) and (9, 3) has slope m = –\(\frac{1}{2}\).
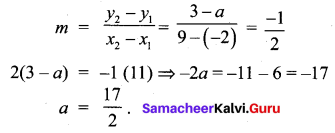
10th Maths Coordinate Geometry Exercise 5.2 Question 8.
The line through the points (-2, 6) and (4, 8) is perpendicular to the line through the points (8, 12) and (x, 24) . Find the value of x.
Solution:

10th Maths Exercise 5.2 In Tamil Question 9.
Show that the given points form a right angled triangle and check whether they satisfies pythagoras theorem
(i) A(1, -4), B(2, -3) and C(4, -7)
(ii) L(0, 5), M(9, 12) and N(3, 14)
Solution:




10th Coordinate Geometry 5.2 Question 10.
Show that the given points form a parallelogram : A(2.5, 3.5), B(10, -4), C(2.5, -2.5) and D(-5, 5)
Solution:
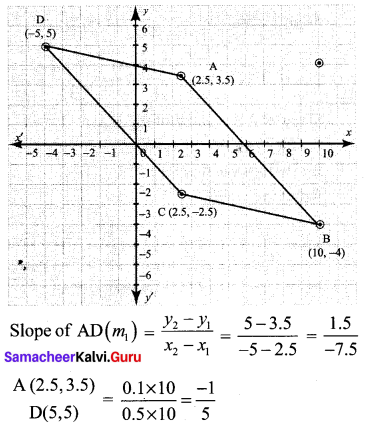

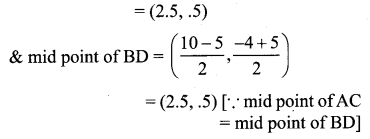
∴ The given points form a parallelogram.
10th Maths 5.2 Exercise Question 11.
If the points A(2, 2), B(-2, -3), C(1, -3) and D(x, y) form a parallelogram then find the value of x and y.
Solution:
A(2, 2), B(-2, -3), C(1, -3), D(x, y)
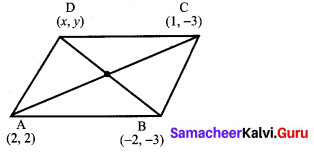
Since ABCD forms a parallelogram, slope of opposite sides are equal and diagonals bisect each other.
Mid point of BD = Mid point of AC
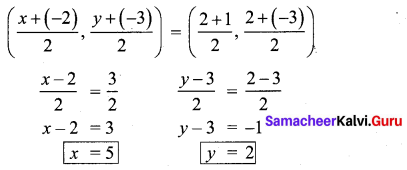
10th Maths 5.2 Question 12.
Let A(3, -4), B(9, -4), C(5, -7) and D(7, -7). Show that ABCD is a trapezium.
Solution:
A (3, -4), B (9, -4), C (5, -7) and D (7, -7)
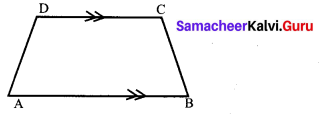
If only one pair of opposite sides of a quadrilateral are parallel, then it is said to be a trapezium.
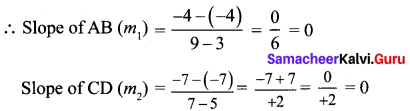
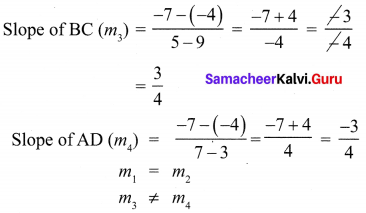
∴ One pair of opposite sides are parallel.
∴ ABCD is a trapezium.
Samacheer Kalvi 10th Maths Exercise 5.2 Question 13.
A quadrilateral has vertices at A(- 4, -2), B(5, -1) , C(6, 5) and D(-7, 6). Show that the mid-points of its sides form a parallelogram
Solution:
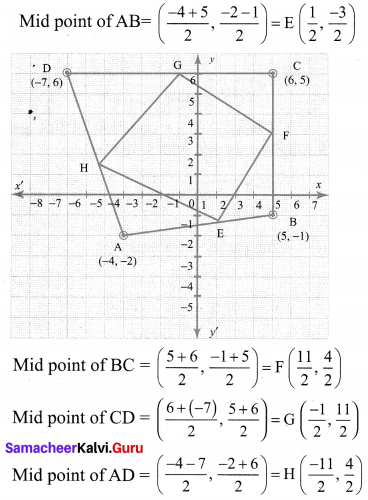
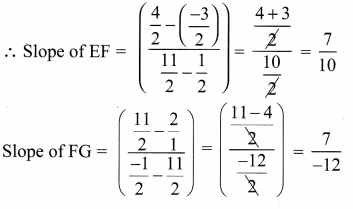
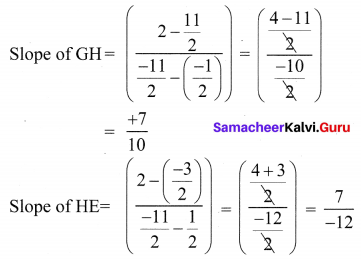

In a parallelogram diagonals bisect each other. Opposite sides are parallel as their slopes are equal the mid points of the diagonals are the same.
∴ Mid points of the sides of a quadrilateral form a parallelogram.
10th Exercise 5.2 Question 14.
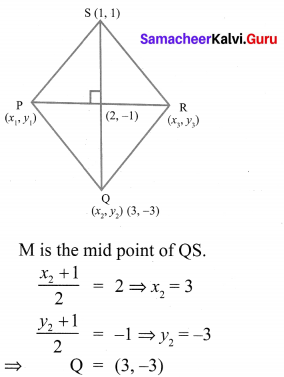
PQRS is a rhombus. Its diagonals PR and QS intersect at the point M and satisfy QS =2PR. If the coordinates of S and M are (1, 1) and (2, -1) respectively, find the coordinates of P.
Solution: