You can Download Samacheer Kalvi 10th Maths Book Solutions Guide Pdf, Tamilnadu State Board help you to revise the complete Syllabus and score more marks in your examinations.
Tamilnadu Samacheer Kalvi 10th Maths Solutions Chapter 3 Algebra Additional Questions
Question 1.
Solve the following system of linear equations in three variables. x + y + z = 6; 2x + 3y + 4z = 20;
3x + 2y + 5z = 22
Solution:
x + y + z = 6 ………….. (1)
2x + 3y + 4z = 20 ………… (2)
3x + 2y + 5z = 22 …………(3)
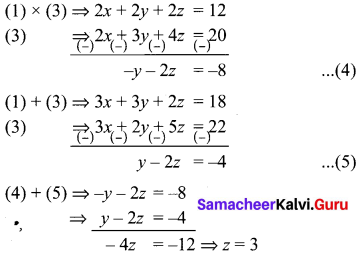
Sub. z = 3 in (5) ⇒ y – 2(3) = -4
y = 2
Sub. y = 2, z = 3 in (1), we get
x + 2 + 3 = 6
x = 1
x = 1, y = 2, z = 3
Question 2.
Using quadratic formula solve the following equations.
(i) p2x2 + (p2 – q2) x – q2 = 0
(ii) 9x2 – 9 (a + b)x + (2a2 + 5ab + 2b2) = 0
Solution:
(i) p2x2 + (p2 – q2)x – q2 = 0
Comparing this with ax2 + bx + c = 0, we have
a = p2
b = p2 – q2
c = -q2
Δ = b2 – 4ac
= (p2 – q2)-4 × p2 × -q2
= (p2 – q2)2 + 4p2 q2
= (p2 + q2)2 > 0
So, the given equation has real roots given by
\(\alpha=\frac{-b-\sqrt{\Delta}}{2 a}=\frac{-\left(p^{2}-q^{2}\right)+\left(p^{2}+q^{2}\right)}{2 p^{2}}=\frac{q^{2}}{p^{2}}\)
\(\beta=\frac{-b-\sqrt{\Delta}}{2 a}=\frac{-\left(p^{2}-q^{2}\right)-\left(p^{2}+q^{2}\right)}{2 p^{2}}\)
= -1
(ii) 9x2 – 9(a + b)x + (2a2 + 5ab + 2b2) = 0
Comparing this with ax2 + bx + c = 0.
a =9
b = -9 (a + b)
c = (2a2 + 5 ab + 2b2)
Δ = B2 – 4AC
⇒ 81 (a + b)2 – 36(2a2 + 5ab + 2b2)
⇒ 9a2 + 9b2 – 18ab
⇒ 9(a – b)2 > 0
∴ the roots are real and given by

Question 3.
Find the HCF of x3 + x2 + x + 1 and x4 – 1.
Answer:
x3 + x2 + x + 1 = x2 (x + 1) + 1 (x + 1)
= (x + 1) (x2 + 1)
x4-1 = (x2)2 – 1
= (x2 + 1) (x2– 1)
= (x2 + 1) (x + 1) (x – 1)
H.C.F. = (x2 + 1)(x + 1)
![]()
Question 4.
Prove that the equation x2(a2 + b2) + 2x(ac + bd) + (c2 + d2) = 0 has no real root if ad ≠ bc
Solution:
Δ = b2 – 4ac
⇒ 4(ac + bd)2 – 4(a2 + b2)(c2 + d2)
⇒ 4[(ac + bd)2 – (a2 + b2)(c2 + d2)]
⇒ 4(a2c2 + b2d2 + 2acbd – a2c2b2c2 – a2d2 – b2d2]
⇒ 4[2acbd – a2d2 – b2c2]
⇒ 4 [a2c2 + b2c2 – 2adbc]
⇒ -4[ad – bc]2
We have ad ≠ bc
∴ ad – bc > 0
⇒ (ad – bc)2 > 0
⇒ -4(ad – bc)2 < 0 ⇒ Δ < 0
Hence the given equation has no real roots.
Question 5.
Find the L.C.M of 2(x3 + x2 – x – 1) and 3(x3 + 3x2 – x – 3)
Answer:
2[x3 + x2 – x – 1] = 2[x2(x+ 1)- 1 (x + 1)]
= 2(x + 1) (x2 – 1)
= 2(x + 1) (x + 1) (x – 1)
= 2(x + 1)2 (x – 1)
3[x3 + 3x2 – x – 3] = 3[x2(x + 3) -1 (x + 3)]
= 3[(x + 3)(x2 – 1)]
= 3(x + 3)(x + 1) (x – 1)
L.C.M. = 6(x + 1)2(x – 1) (x + 3)
Question 6.
A two digit number is such that the product of its digits is 12. When 36 is added to the number the digits interchange their places. Find the number.
Solution:
Let the ten’s digit of the number be x. It is given that the product of the digits is 12.
Unit’s digit = \(\frac{12}{x}\)
Number = 10x + \(\frac{12}{x}\)
If 36 is added to the number the digits interchange their places.
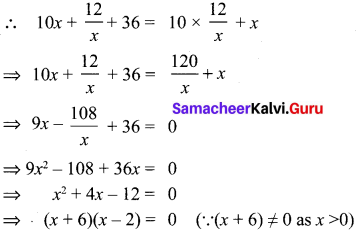
x = -6, 2.
But a number can never be (-ve). So, x = 2.
The number is 10 × 2 + \(\frac{12}{2}\) = 26
Question 7.
Seven years ago, Vanin’s age was five times the square of swati’s age. Three years hence Swati’s age will be two fifth of Varun’s age. Find their present ages.
Solution:
Seven years ago, let Swathi’s age be x years.
Seven years ago, let Varun’s age was 5x2 years.
Swathi’s present age = x + 7 years
Varun’s present age = (5x2 + 7) years
3 years hence, we have Swathi’s age = x + 7 + 3 years
= x + 10 years
Varun’s age = 5x2 + 7 + 3 years
= 5x2 + 10 years
It is given that 3 years hence Swathi’s age will be \(\frac{2}{5}\) of Varun’s age.
∴ x + 10 = \(\frac{2}{5}\) (5x2 + 10)
⇒ x + 10 = 2x2 + 4
⇒ 2x2 – x – 6 = 0
⇒ 2x(x – 2) + 3(x – 2) = 0
⇒ (2x + 3)(x – 2) = 0
⇒ x – 2 = 0
⇒ x = 2 (∵ 2x + 3 ≠ 0 as x > 0)
Hence Swathi’s present age = (2 + 7) years
= 9 years
Varun’s present age = (5 × 22 + 7) years = 27 years
![]()
Question 8.
A chess board contains 64 equal squares and the area of each square is 6.25 cm2. A border round the board is 2 cm wide find its side.
Solution:
Let the length of the side of the chess board be x cm. Then,
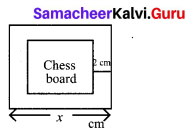
Area of 64 squares = (x – 4)2
(x – 4)2 = 64 × 6.25
⇒ x2 – 8x+ 16 = 400
⇒ x2 – 8x-384 = 0
⇒ x2 – 24x + 16x – 384 = 0
⇒ (x – 24)(x + 16) = 0
⇒ x = 24 cm.
Question 9.
Find two consecutive natural numbers whose product is 20.
Solution:
Let a natural number be x.
The next number = x + 1
x (x + 1) = 20
x2 + x – 20 = 0
(x + 5)(x – 4) = 0
x = -5, 4
∴ x = 4 (∵ x ≠ -5, x is natural number)
The next number = 4 + 1 = 5
Two consecutive numbers are 4, 5
Question 10.
A two digit number is such that the product of its digits is 18, when 63 is subtracted from the number, the digits interchange their places. Find the number.
Solution:
Let the tens digit be x. Then the units digits = \(\frac{18}{x}\)
