Samacheer Kalvi 10th Maths Solutions Chapter 2 Numbers and Sequences Ex 2.10

You can Download Samacheer Kalvi 10th Maths Book Solutions Guide Pdf, Tamilnadu State Board help you to revise the complete Syllabus and score more marks in your examinations.

Tamilnadu Samacheer Kalvi 10th Maths Solutions Chapter 2 Numbers and Sequences Ex 2.10

Multiple choice questions
Question 1.
Euclid’s division lemma states that for positive integers a and b, there exist unique integers q and r such that a = bq + r, where r must satisfy.
(1) 1 < r < b
(2) 0 < r < b
(3) 0 < r < b
(4) 0 < r < b
Answer:
(3) 0 < r < b

Question 2.
Using Euclid’s division lemma, if the cube of any positive integer is divided by 9 then the possible remainders are
(1) 0, 1, 8
(2) 1, 4, 8
(3) 0, 1, 3
(4) 1, 3, 5
Answer:
(1) 0,1,8
Hint:
Cube of any +ve integers 1³, 2³, 3³, 4³,. . .
1, 8, 27, 64, 125, 216 …
Remainders when 27, 64, 125 are divided by 9.

Question 3.
If the H.C.F of 65 and 117 is expressible in the form of 65m -117 , then the value of m is ………………….
(1) 4
(2) 2
(3) 1
(4) 3
Answer:
(2) 2
Hint:
117 = 3 × 3 × 13
65 = 5 × 13
H.C.F = 13
65m – 117 = 13 ⇒ 65m = 117 + 13 = 130
m = \(\frac { 130 }{ 65 } \) = 2
The value of m = 2

Question 4.
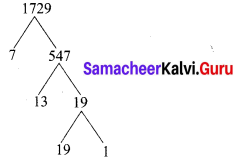
The sum of the exponents of the prime factors in the prime factorization of 1729 is
(1) 1
(2) 2
(3) 3
(4) 4
Answer:
(3) 3
Hint:
1729 = 7¹ × 13¹ × 19¹

Question 5.
The least number that is divisible by all the numbers from 1 to 10 (both inclusive) is
(1) 2025
(2) 5220
(3) 5025
(4) 2520
Answer:
(4) 2520
Hint:

∴ L.C.M. of 1,2,3,4,…,10 is 2 × 2 × 3 × 5 × 7 × 2 × 3 = 2520

Question 6.
7^4k ≡ …………………. (mod 100)
(1) 1
(2) 2
(3) 3
(4) 4
Answer:
(1) 1
Hint:
7^4k ≡ . . . . . (mod 100)
7^4k = (7⁴)^k ≡ ……….. (mod 100) (7⁴ – 2401)
The value is 1.

Question 7.
Given F₁ = 1, F₂ = 3 and Fn = F_n-1 + F_n-2 then
(1) 3
(2) 5
(3) 8
(4) 11
Answer:
(4) 11
Answer:
F₁ = 1, F₂ = 3
F_n = F_n-1 + F_n-2
F₅ = F_5-1 + F_5-2 = F₄ + F₃
= F₃ + F₂ + F₂ + F₁
= F₂ + F₁ + F₂ + F₂ + F₁
= 3 + 1 + 3 + 3 + 1 = 11

Question 8.
The first term of an arithmetic progression is unity and the common difference is 4. Which of the following will be a term of this A.P …………..
(1) 4551
(2) 10091
(3) 7881
(4) 13531
Answer:
(3) 7881
Hint:
Here a = 1, d = 4
t_n = a + (n – 1) d = 1 + (n – 1) 4
= 1 + 4n – 4
= 4n – 3
4554
(i) 4n – 3 = 4551 ⇒ 4n = 4551 + 3 ⇒ n = \(\frac { 4554 }{ 4 } \) = 1138.5.
It is not a term of A.P.

(ii) 4n – 3 = 10091 ⇒ 4n = 10091 + 3 = 10094
n = \(\frac { 10094 }{ 4 } \) = 2523.5 it is a term of A.P.

(iii) 4n – 3 = 7881 ⇒ 4n = 7881 + 3
n = \(\frac { 7884 }{ 4 } \) = 1971.
∴ 7881 is a term of the A.P.

Question 9.
If 6 times of 6^th term of an A.P is equal to 7 times the 7th term, then the 13th term of the A.P. is
(1) 0
(2) 6
(3) 7
(4) 13
Answer:
(1) 0
Hint:
6t₆ = 7t₇
6(a + 5d) = 7(a + 6d)
6a + 30d = 7a + 42d
7a + 42d – 6a – 30d = 0
a + 12d = 0 = t₁₃

Question 10.
An A.P consists of 31 terms. If its 16^th term is m, then the sum of all the terms of this A.P. is …………..
(1) 16m
(2) 62m
(3) 31m
(4) \(\frac { 31 }{ 2 } \)m
Answer:
(3) 31m
Hint:
M = 31
t₁₆ = m ⇒ a + 15d = m
S_n = \(\frac { n }{ 2 } \)[2a + (n – 1)d]
S_n = \(\frac { 31 }{ 2 } \)[2a + 30d]= \(\frac { 31 }{ 2 } \) × 2[a + 15d]
= 31 (m) = 31m

Question 11.
In an A.P., the first term is 1 and the common difference is 4. How many terms of the A.P must be taken for their sum to be equal to 120?
(1) 6
(2) 7
(3) 8
(4) 9
Answer:
(3) 8
Hint:

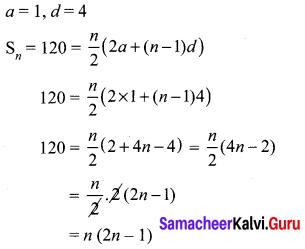
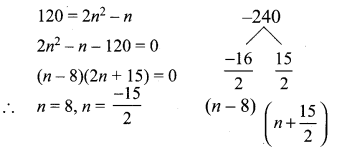
Question 12.
If A = 2⁶⁵ and B = 2⁶⁴ + 2⁶³ + 2⁶² + +2⁰ which of the following is true?
(1) B is 264 more than A
(2) A and B are equal
(3) B is larger than A by 1
(4) A is larger than B by 1
Answer:
(4) A is larger than B by 1
Hint:
A = 2⁶⁵
B = 2⁶⁴ + 2⁶³ + 2⁶² + … + 20
B = 2⁰ + 2¹ + 2² + … + 264
G.P = 1 + 2¹ + 2² + … + 2⁶⁴ it is a G.P
Here a = 1, r = 2, n = 65

A = 2⁶⁵, B = 2⁶⁵ – 1
∴ B is smaller.
A is larger than B by 1.

Question 13.
The next term of the sequence \(\frac { 3 }{ 16 } \),\(\frac { 1 }{ 8 } \),\(\frac { 1 }{ 12 } \),\(\frac { 1 }{ 18 } \), ….
(1) \(\frac { 1 }{ 24 } \)
(2) \(\frac { 1 }{ 27 } \)
(3) \(\frac { 2 }{ 3 } \)
(4) \(\frac { 1 }{ 81 } \)
Answer:
(2) \(\frac { 1 }{ 27 } \)
Hint:

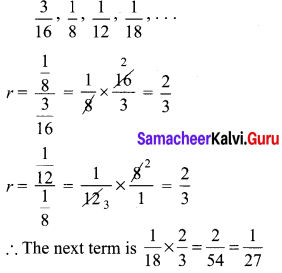
Question 14.
If the sequence t₁, t₂, t₃, …………are in A.P. then the sequence t₆, t₁₂, t₁₈, …… is ………….
(1) a Geometric progression
(2) an Arithmetic progression
(3) neither an Arithmetic progression nor a Geometric progression
(4) a constant sequence
Answer:
(2) an Arithmetic progression
Hint: t₁, t₂, t₃ …. are in A.P
t₆, t₁₂, t₁₈ …… is also an A.P. (6, 12, 18 …….. is an A.P.)

Question 15.
The value of (1³ + 2³ + 3³ + … + 15³) – (1 + 2 + 3 + … + 15) is
(1) 14400
(2) 14200
(3) 14280
(4) 14520
Answer:
(3) 14280
Hint:
\(\left(\frac{15 \times 16}{2}\right)^{2}-\frac{15 \times 16}{2}\) = (120)² – 120 = 14280