Samacheer Kalvi 10th Maths Solutions Chapter 1 Relations and Functions Unit Exercise 1

You can Download Samacheer Kalvi 10th Maths Book Solutions Guide Pdf, Tamilnadu State Board help you to revise the complete Syllabus and score more marks in your examinations.

Tamilnadu Samacheer Kalvi 10th Maths Solutions Chapter 1 Relations and Functions Unit Exercise 1

10th Maths Unit Exercise 1 Question 1.
If the ordered pairs (x² – 3x, y² + 4y) and (-2, 5) are equal, then find x and y.
Solution:
(x² – 3x, y² + 4y) = (-2, 5)
x² – 3x = -2
x² – 3x + 2 = 0

10th Maths Chapter 1 Unit Exercise Question 2.
The cartesian product A × A has 9 elements among which (-1, 0) and (0,1) are found.
Find the set A and the remaining elements of A × A.
Answer:
n(A × A) = 9
n(A) = 3
A = {-1,0,1}
A × A = {-1, 0, 1} × {-1, 0, 1}
A × A = {(-1,-1)(-1, 0) (-1, 1)
(0, -1) (0, 0) (0, 1)
(1,-1) (1, 0) (1, 1)}
The remaining elements of A × A =
{(-1, -1) (-1, 1) (0, -1) (0, 0) (1,-1) (1,0) (1,1)}

10th Maths Unit 1 Question 3.
Given that

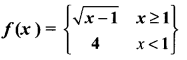
(i) f(0)
(ii) f(3)
(iii) f(a + 1) in terms of a.(Given that a > 0)
Solution:
(i) f(0) = 4
(ii) f(3) = \(\sqrt{3-1}=\sqrt{2}\)
(iii) f(a + 1) = \(\sqrt{a+1-1}=\sqrt{a}\)

Samacheer Kalvi 10th Maths Book Solutions Question 4.
Let A = {9,10,11,12,13,14,15,16,17} and let f : A → N be defined by f(n) = the highest prime factor of n ∈ A. Write f as a set of ordered pairs and find the range of f.
Answer:
A= {9, 10, 11, 12, 13, 14, 15, 16, 17}
f: A → N
f(x) = the highest prime factor n ∈ A
f = {(9, 3) (10, 5) (11, 11) (12, 3) (13, 13) (14, 7) (15, 5) (16, 2) (17, 17)}
Range of f = {3, 5, 11, 13, 7, 2, 17}
= {2, 3, 5, 7, 11, 13, 17}

10th Maths Exercise 1.1 Samacheer Kalvi Question 5.
Find the domain of the function f(x) = \(\sqrt{1+\sqrt{1-\sqrt{1-x^{2}}}}\)
Solution:
f(x) = \(\sqrt{1+\sqrt{1-\sqrt{1-x^{2}}}}\)
Domain of f(x) = {-1, 0, 1}
(x² = 1, -1, 0, because \(\sqrt{1-x^{2}}\) should be +ve, or 0)

10th Maths Unit Exercise Solutions Question 6.
If f (x) = x², g(x) = 3x and h(x) = x – 2, Prove that (f o g)o h = f o(g o h).
Answer:
f(x) = x² ; g(x) = 3x and h(x) = x – 2
L.H.S. = (fog) oh
fog = f[g(x)]
= f(3x)
= (3x)² = 9x²
(fog) oh = fog[h(x)]
= fog (x – 2)
= 9(x – 2)²
= 9[x² – 4x + 4]
= 9x² – 36x + 36 ….(1)
R.H.S. = fo(goh)
goh = g [h(x)]
= g(x – 2)
= 3(x – 2)
= 3x – 6
fo(goh) = fo [goh (x)]
= f(3x – 6)
= (3x – 6)²
= 9x² – 36x + 36 ….(2)
From (1) and (2) we get
L.H.S. = R.H.S.
(fog) oh = fo {goh)

Samacheer Kalvi 10th Maths Exercise 1.1 Question 7.
A = {1, 2} and B = {1, 2, 3, 4} , C = {5, 6} and D = {5, 6, 7, 8} . Verify whether A × C is a subset of B × D?
Solution:
A = {1, 2), B = (1, 2, 3, 4)
C = {5, 6}, D = {5, 6, 7, 8)
A × C = {(1, 5), (1, 6), (2, 5), (2, 6)}
B × D = {(1, 5), (1, 6), (1, 7), (1, 8), (2, 5), (2, 6), (2, 7), (2, 8), (3, 5), (3, 6), (3, 7), (3, 8), (4, 5), (4, 6), (4, 7), (4, 8)}
(A × C) ⊂ (B × D) It is proved.

10th Maths Unit 1 Question Paper Question 8.
If f(x) = \(\frac{x-1}{x+1}\), x ≠ 1 show that f(f(x)) = \(-\frac{1}{x}\), Provided x ≠ 0.
Solution:

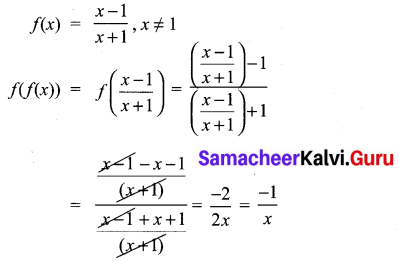
Hence it is proved.

10th Maths Unit Exercise Question 9.
The function/and g are defined by f(x) = 6x + 8; g(x) = \(\frac{x-2}{3}\).
(i) Calculate the value of \(gg\left(\frac{1}{2}\right)\)
(ii) Write an expression for g f(x) in its simplest form.
Solution:

10th Maths Chapter 1 Samacheer Kalvi Question 10.
Write the domain of the following real functions

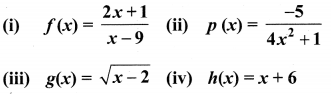
Solution:
(i) f(x) = \(\frac{2x+1}{x-9}\)
The denominator should not be zero as the function is a real function.
∴ The domain = R – {9}
(ii) p(x) = \(\frac{-5}{4 x^{2}+1}\)
The domain is R.
(iii) g(x) = \(\sqrt{x-2}\)
The domain = [2, ∝)
(iv) h(x) = x + 6
The domain is R.