You can Download Samacheer Kalvi 12th Maths Book Solutions Guide Pdf, Tamilnadu State Board help you to revise the complete Syllabus and score more marks in your examinations.
Tamilnadu Samacheer Kalvi 12th Maths Solutions Chapter 3 Theory of Equations Ex 3.1
Exercise 3.1 Class 12 Maths State Board Question 1.
If the sides of a cubic box are increased by 1, 2, 3 units respectively to form a cuboid, then the volume is increased by 52 cubic units. Find the volume of the cuboid.
Solution:
Let the side of the cube be ‘x’
Sides of cuboid are (x + 1) (x + 2) (x + 3)
∴ Volume of cuboid = x3 + 52
⇒ (x + 1) (x + 2) (x + 3) = x3 + 52
⇒ (x2 + 3x + 2)(x + 3) = x3 + 52
⇒ x3 + 3x2 + 3x2 + 9x + 2x + 6 – x3 – 52 = 0
⇒ 6x2 + 11x – 46 = 0 (÷2)
⇒ (x – 2) (6x + 23) = 0
⇒ x – 2 = 0 or 6x + 23 = 0
⇒ x = 2 or x = \(-\frac{23}{6}\) (not possible)
∴ x = 2
Volume of cube = 23 = 8
Volume of cuboid = 52 + 8 = 60 cubic units
12th Maths Exercise 3.1 Question 2.
Construct a cubic equation with roots
(i) 1, 2 and 3
(ii) 1, 1 and -2
(iii) 2, \(\frac { 1 }{ 2 }\) and 1
Solution:
(i) Given roots are α = 1, β = 2, γ = 3
The cubic equation is
x3 – x2 (α + β + γ) + x (αβ + βγ + γα) – αβγ = 0
⇒ x3 – x2 (1 + 2 + 3) + x (2 + 6 + 3) – (1) (2) (3) = 0
⇒ x3 – 6x2 + 11x – 6 = 0
(ii) α = 1, β = 1, γ = -2
The cubic equation is
x3 – x2 (α + β + γ) + x (αβ + βγ + γα) – αβγ = 0
⇒ x3 – x2 (1 + 1 – 2) + x (1 – 2 – 2) – (1) (1) (-2) = 0
⇒ x3 – 0x2 – 3x + 2 = 0
⇒ x3 – 3x + 2 = 0
(iii) α = 2, β = \(\frac { 1 }{ 2 }\), γ = 1
The cubic equation is
x3 – x2 (α + β + γ) + x (αβ + βγ + γα) – αβγ = 0
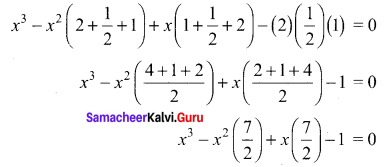
2x3 – 7x2 + 7x – 2 = 0
12th Maths Theory Of Equations Question 3.
If α, β and γ are the roots of the cubic equation x3 + 2x2 + 3x + 4 = 0, form a cubic equation whose roots are
(i) 2α, 2β, 2γ
(ii) \(\frac{1}{\alpha}, \frac{1}{\beta}, \frac{1}{\gamma}\)
(iii) -α, -β, -γ
Solution:
(i) Given that α, β, γ are the roots of x3 + 2x2 + 3x + 4 = 0
Compare with x3 + bx2 + cx + d = 0
b = 2, c = 3, d = 4
α + β + γ = -6 = -2
αβ + βγ + γα = c = 3
αβγ = -d = -4
Given roots are 2α, 2β, 2γ
2α + 2β + 2γ = 2 (α + β + γ)
= 2 (-2)
= -4
(2α) (2β) + (2β) (2γ) + (2γ) (2α) = (4αβ + 4βγ + 4γα)
= 4(αβ + βγ + γα)
= 4(3)
= 12
(2α) (2β) (2γ) = 8(αβγ)
= 8(-4)
= -32
The equation is
x3 – x2 (2α + 2β + 2γ) + x (4αβ + 4βγ + 4γα) – 8 (αβγ) = 0
⇒ x3 – x2 (-4) + x (12) – (-32) = 0
⇒ x3 + 4x2 + 12x + 32 = 0
(ii) The given roots are \(\frac{1}{\alpha}, \frac{1}{\beta}, \frac{1}{\gamma}\)
The cubic equation is

4x3 + 3x2 + 2x + 1 = 0 (Multiply by 4)
(iii) The given roots are -α, -β, -γ
The cubic equation is
x3 – x2 (-α – β – γ) + x (αβ + βγ + γα) + (αβγ) = 0
⇒ x3 + x2 (α + β + γ) + x (αβ + βγ + γα) + (αβγ) = 0
⇒ x3 + x2 (-2) + x (3) – 4 = 0
⇒ x3 – 2x2 + 3x – 4 = 0
12th Maths Chapter 3 Exercise 3.1 Question 4.
Solve the equation 3x3 – 16x2 + 23x – 6 = 0 if the product of two roots is 1.
Solution:
The given equation is 3x3 – 16x2 + 23x – 6 = 0
⇒ \(x^{3}-\frac{16}{3} x^{2}+\frac{23}{3} x-2=0\) (÷3)
Let the roots be α, β, γ
α + β + γ = -b = \(\frac{16}{3}\) …….. (1)
αβ + βγ + γα = c = \(\frac{23}{3}\) …….. (2)
αβγ = -d = 2 ……. (3)
Given that αβ = 1
from (3), γ = 2
Substitute \(\beta=\frac{1}{\alpha}\), γ = 2 in (1)
⇒ \(\alpha+\frac{1}{\alpha}+2=\frac{16}{3}\)
\(\Rightarrow \frac{\alpha^{2}+1}{\alpha}=\frac{16}{3}-2\)
⇒ \(\frac{\alpha^{2}+1}{\alpha}=\frac{10}{3}\)
⇒ 3α2 + 3 = 10α
⇒ 3α2 – 10α + 3 = 0
⇒ (3α – 1) (α – 3) = 0
⇒ α = \(\frac{1}{3}\), 3
α = \(\frac{1}{3}\), β = 3 (or) when a = 3, β = \(\frac{1}{3}\)
∴ The roots are 3, \(\frac{1}{3}\), 2
(or) when γ = 2, by synthetic division method.
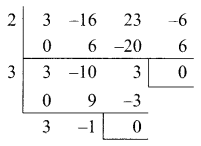
The factors are (x – 2) (x – 3) (3x – 1)
∴ The roots are 2, 3, \(\frac{1}{3}\)
12th Maths 3.1 Question 5.
Find the sum of squares of roots of the equation 2x4 – 8x3 + 6x2 – 3 = 0.
Solution:
The given equation is 2x4 – 8x3 + 6x2 – 3 = 0.
(÷ 2) ⇒ x4 – 4x3 + 3x2 – \(\frac{3}{2}\) = 0
Let the roots be α, β, γ, δ
α + β + γ + δ = -b = 4
(αβ + βγ + γδ + αδ + αγ + βδ) = c = 3
αβγ + βγδ + γδα = -d = 0
αβγδ = \(\frac{-3}{2}\)
To Find α2 + β2 + γ2 + δ2 = (α + β + γ + δ)2 – 2 (αβ + βγ + γδ + αδ + αγ + βδ)
= (4)2 – 2(3)
= 16 – 6
= 10
12 Maths Exercise 3.1 Question 6.
Solve the equation x3 – 9x2 + 14x + 24 = 0 if it is given that two of its roots are in the ratio 3 : 2.
Solution:
The given equation is x3 – 9x2 +14x + 24 = 0.
Since the two roots are in the ratio 3 : 2.
The roots are α, 3λ, 2λ
α + 3λ + 2λ = -b = 9
⇒ α + 5λ = 9 …… (1)
(α) (3λ) (2λ) = -24
6λ2α = -24
⇒ λ2α = -4 …… (2)
(1) ⇒ α = 9 – 5λ
(2) ⇒ λ2 (9 – 5λ) = -4
9λ2 – 5λ3 + 4 = 0
5λ3 – 9λ2 – 4 = 0
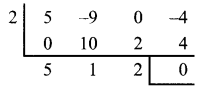
(λ – 2) (5λ2 + λ + 2) = 0
λ = 2, 5λ2 + λ + 2 = 0 has only Imaginary roots Δ < 0
when λ = 2, α = 9 – 5 (2) = 9 – 10 = -1
The roots are α, 3λ, 2λ i.e., -1, 6, 4
Samacheer Kalvi Guru 12th Maths Question 7.
If α, β and γ are the roots of the polynomial equation ax3 + bx2 + cx + d= 0, find the value of \(\Sigma \frac{\alpha}{\beta \gamma}\) in terms of the coefficients.
Solution:
The given equation is ax3 + bx2 + cx + d = 0.
÷a ⇒ \(x^{3}+\frac{b}{a} x^{2}+\frac{c}{a} x+\frac{d}{a}=0\)
Let the roots be α, β, γ
α + β + γ = \(-\frac{b}{a}\)
αβ + βγ + γα = \(\frac{c}{a}\)
αβγ = \(-\frac{d}{a}\)
To find:
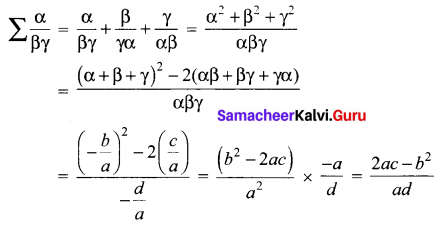
Samacheer Kalvi 12 Maths Solutions Question 8.
If α, β, γ and δ are the roots of the polynomial equation 2x4 + 5x3 – 7x2 + 8 = 0, find a quadratic equation with integer coefficients whose roots are α + β + γ + δ and αβγδ.
Solution:
The given equation is 2x4 + 5x3 – 7x2 + 8 = 0.
÷ 2 ⇒ \(x^{4}+\frac{5}{2} x^{3}-\frac{7}{2} x^{2}+4=0\)
Let the roots be α, β, γ, δ
α + β + γ + δ = \(-\frac{5}{2}\)
αβγδ = -4
To form the quadratic equation with the given roots α + β + γ + δ, αβγδ.
x2 – x(S.O.R) + P.O.R = 0
\(x^{2}-x\left(\frac{-5}{2}-4\right)+\left(\frac{-5}{2}\right)(-4)=0\)
\(\Rightarrow x^{2}-x\left(\frac{-13}{2}\right)+10=0\)
2x2 + 13x + 20 = 0
Samacheer Kalvi 12th Maths Solutions Question 9.
If p and q are the roots of the equation lx2 + nx + n = 0, show that \(\sqrt{\frac{p}{q}}+\sqrt{\frac{q}{p}}+\sqrt{\frac{n}{l}}=0\)
Solution:
The given equation is lx2 + nx + n = 0.
p + q = \(-\frac{n}{l}\), pq = \(\frac{n}{l}\)
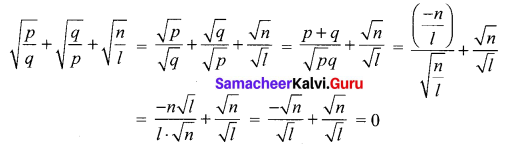
Samacheer Kalvi.Guru 12th Maths Question 10.
If the equations x2 + px + q = 0 and x2 + p’x + q’ = 0 have a common root, show that it must be equal to \(\frac{p q^{\prime}-p^{\prime} q}{q-q^{\prime}}\) or \(\frac{q-q^{\prime}}{p^{\prime}-p}\)
Solution:
If α is the common root, then.
α2 + pα + q = 0 ……. (1)
α2 + p’α + q’ = 0 ……… (2)
Subtracting α (p – p’) = q’ – q
\(\alpha=\frac{q^{\prime}-q}{p-p^{\prime}}=\frac{q-q^{\prime}}{p^{\prime}-p}\) …….. (3)
Eliminating α from (1) & (2)

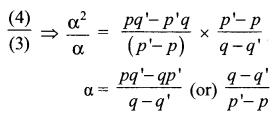
Samacheer Kalvi Class 12 Maths Solutions Question 11.
Formulate into a mathematical problem to find a number such that when its cube root is added to it, the result is 6.
Solution:
Let the number be x.
Given that \(\sqrt[3]{x}+x=6\)
\(\Rightarrow \sqrt[3]{x}=6-x\)
Cubing on both sides
x = (6 – x)3
⇒ x = 216 – 3 (6)2 (x) + 3(6) (x)2 – x3
⇒ x = 216 – 108x + 18x2 – x3
⇒ x3 – 18x2 + 109x – 216 = 0
Samacheerkalvi.Guru 12th Maths Question 12.
A 12 metre tall tree was broken into two parts. It was found that the height of the part which was left standing was the cube root of the length of the part that was cut away. Formulate this into a mathematical problem to find the height of the part which was cut away.
Solution:
Let the two parts be x and (12 – x)
Given that \(x=\sqrt[3]{12-x}\)
Cubing on both side,
x3 = 12 – x
⇒ x3 + x – 12 = 0
Samacheer Kalvi 12th Maths Solutions Chapter 3 Theory of Equations Ex 3.1 Additional Problems
Samacheer Kalvi 12th Maths Example Sums Question 1.
Construct a cubic equation with roots 2, 3, 4.
Solution:
Given roots are 2, 3, 4
Take α = 1; β = 3; γ = 4
The required cubic polynomial is
x3 – (α + β + γ) x2 + (αβ + βγ + γα) x – αβγ = 0
x3 – (1 + 3 + 4)x2 + (3 + 12 + 4) x – 12 = 0
x3 – 8x2 + 19 x – 12 = 0
Samacheer Kalvi 12th Maths Question 2.
If α, β, γ are the roots of the cubic equation x3 – 6x2 + 11x – 6 = 0. From a cubic equation whose roots are 2α, 2β, 2γ.
Solution:
Given that α, β, γ are the roots of x3 – 6x2 + 11x – 6 = 0 … α, β, γ
α + β + γ = 6 …(1)
αβ + βγ + γα = 11 …(2)
αβγ = 6 …(3)
Form a cubic equation whose roots are 2α, 2β, 2γ.
∴ 2α + 2β + 2γ = 2(α + β + γ) = 2(6) = 12
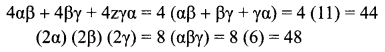
The required cubic equation is
x3 – (2α + 2β + 2γ)x2 + (4αβ + 4βγ + 4γα) x – (2α) (2β) (2γ) = 0
x3 – 12x2 + 44x – 48 = 0
Samacheer Kalvi Maths 12th Question 3.
If the roots of x4 + 5x3 – 30x2 – 40x + 64 = 0 are in G.P; then find the roots.
Solution:

Samacheer Kalvi 12th Maths Guide Question 4.
Determine the value of k such that the equation (2k – 5)x2 – 4x – 15 = 0 and (3k – 8)x2 – 5x – 21 = 0 may have a common root.
Solution:
If α be the common root, the two equations.
(2k – 5) α2 – 4α – 15 = 0
(3k – 8) α2 – 5α – 21 = 0 These are the linear equation is α2 and α.
By cross multiplication rule
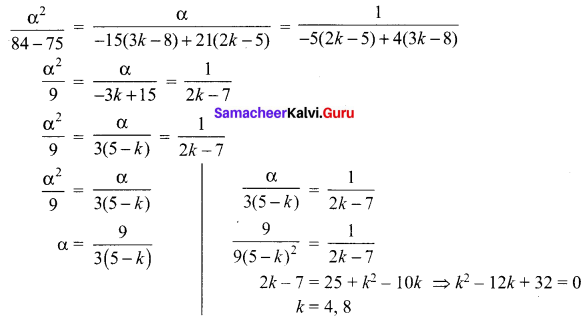
12th Maths Samacheer Kalvi Question 5.
If α, β, γ are the roots of the equation x3 + px2 + qx +1 = 0. Find the value of the following in terms of coefficients.
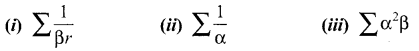
Solution:

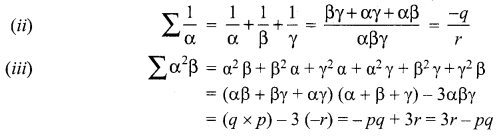
Samacheer Kalvi Guru 12 Maths Question 6.
![]()
Solution:
