Samacheer Kalvi 9th Maths Guide Chapter 6 முக்கோணவியல் Ex 6.4

Tamilnadu State Board New Syllabus Samacheer Kalvi 9th Maths Guide Pdf Chapter 6 முக்கோணவியல் Ex 6.4 Textbook Questions and Answers, Notes.

TN Board 9th Maths Solutions Chapter 6 முக்கோணவியல் Ex 6.4

கேள்வி 1.
கீழ்க்காண்பனவற்றின் மதிப்புகளைக் காண்க.
i) sin49°
ii) cos 74°39^|
iii) tan 54°26^|
iv) sin 21°21^|
v) cos 33°53^|
vi) tan 70° 17^|
விடை:
i) sin49° = 0.7547
ii) cos 74°39^| = 0.2648
iii) tan 54° 26^| = 1.3985
iv) sin 21°21^| = 0.3641
v) cos 33°53^| = 0.8302
vi) tan 70° 17^| = 2.7907

கேள்வி 2.
θ இன் மதிப்பு காண்க.
i) sin θ = 0.9975
ii) cos θ = 0.6763
iii) tan θ = 0.0720
iv) cos θ = 0.0410
v) tan θ = 7.5958
விடை:
i) sin θ = 0.9975
θ = sin^-1 (0.9975)
= 85°57^|

ii) cos θ = 0.6763
θ = cos^-1 (0.6763)
= 47° 27^|

iii) tan θ = 0.0720
θ = tan^-1 (0.0720)
= 4° 7^|

iv) cos θ = 0.0410
θ = cos^-1 (0.0410)
= 87°39^|

v) tan θ = 7.5958
θ = tan^-1 (7.5958)
= 82°30^|

கேள்வி 3.
கீழ்க்காண்பனவற்றின் மதிப்பு காண்க.
i) sin 65°39^| + cos 24°57^| + tan10°10^|
ii) tan 70° 58^| + cos 15° 26^| – sin 84°59^|
விடை:
i) sin 65°39^| + cos 24°57^| + tan10°10^|
= 0.911 + 0.9066 + 0.1793
= 1.9970

ii) tan 70°58^| + cos 15° 26^| – sin 84°59^|
= 2.8982 + 0.9639 – 0.9962
= 3.8621 – 0.9962
= 2.8659

கேள்வி 4.
கர்ணம் 10 செ.மீ. மற்றும் ஒரு குறுங்கோண அளவு 24° 24^| கொண்ட ஒரு செங்கோண முக்கோணத்தின் பரப்பு காண்க.
விடை:

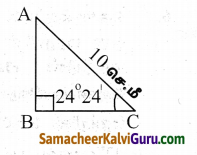
sin θ = \(\frac{\mathrm{AB}}{\mathrm{AC}}\)
sin 24°24^| = \(\frac{\mathrm{AB}}{10}\)
0.4131 x 10 = AB
4.131 = AB
AB= 4.131 செ.மீ.
cos = \(\frac{B C}{A C}\)
cos 24° 24^| = \(\frac{\mathrm{BC}}{10}\)
0.9107 = \(\frac{\mathrm{BC}}{10}\)
9.107 = BC
BC = 9.107 செ.மீ.
செங்கோண முக்கோணத்தின் பரப்பளவு
= \(\frac{1}{2}\) bh ச. அலகுகள்
= \(\frac{1}{2}\) × BC × AB செ.மீ.²
= \(\frac{1}{2}\) × 9.107 × 4.131 செ.மீ.²
= 18.81 செ.மீ.²

கேள்வி 5.
5 மீ நீளமுள்ள ஓர் ஏணியானது சுவற்றிலிருந்து 4 மீ தொலைவில் அடிப்பாகம் தரையைத் தொடுமாறு சுவற்றின் மீது சாய்த்து வைக்கப்பட்டுள்ளது எனில், ஏணி தரைப்பகுதியுடன் ஏற்படுத்தும் கோணம் காண்க.
விடை:

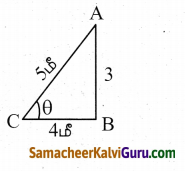
cos θ = \(\frac{4}{5}\)
θ = \(\cos ^{-1}\left(\frac{4}{5}\right)\)
= cos^-1 (0.8)
θ = 36°52^|

கேள்வி 6.
கொடுக்கப்பட்ட படத்தில் HT என்பது நேரான ஒரு மரத்தின் உயரத்தைக் குறிக்கிறது. மரத்தின் அடிப்பாகத்திலிருந்து 60மீ தொலைவிலுள்ள P என்ற புள்ளியிலிருந்து மரத்தின் உச்சியின் ஏற்றக் கோணம் (∠P) 42° எனில், மரத்தின் உயரத்தைக் காண்க.
விடை:

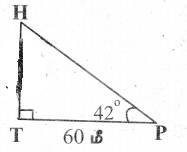
tan 42° = \(\frac{\mathrm{HT}}{60}\)
0.9004 = \(\frac{\mathrm{HT}}{60}\)
0.9004 × 60 = HT
HT = 54.02
மரத்தின் உயரம் = 54.02 மீ