You can Download Samacheer Kalvi 9th Maths Book Solutions Guide Pdf, Tamilnadu State Board help you to revise the complete Syllabus and score more marks in your examinations.
Tamilnadu Samacheer Kalvi 9th Maths Solutions Chapter 4 Geometry Ex 4.5
9th Maths Geometry Exercise 4.5 Question 1.
Construct the ∆LMN such that LM = 7.5 cm, MN = 5 cm and LN = 8 cm. Locate its centroid.
Solution:
In ∆LMN
LM = 7.5 cm,
MN = 5 cm,
LN = 8 cm
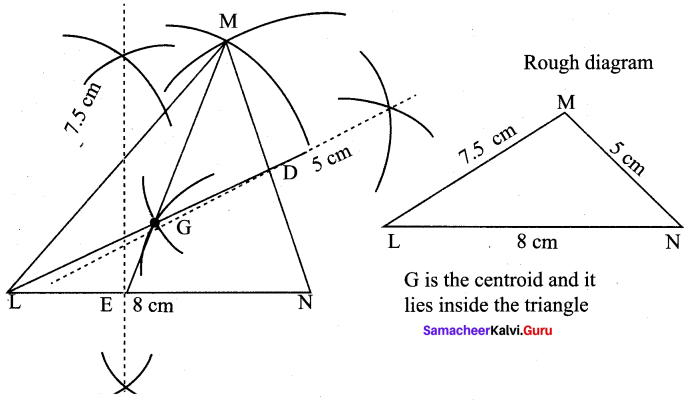
Construction :
Step 1 : Draw ∆LMN with LNM = 8 cm, MN = 5 cm, LM = 7.5 cm
Step 2 : Construct perpendicular bisectors for any two sides (LN and MN) to find the mid points of LM and MN.
Step 3 : Draw the medians LD, ME. Let them meet at G.
Step 4 : G is the centroid of the triangle LMN.
9th Maths Geometry Question 2.
Draw and locate the centroid of the triangle ABC where right angle at A, AB = 4 cm and AC = 3 cm.
Solution:
In ∆ABC,
AB = 4 cm,
AC = 3 cm,
∠A = 90°
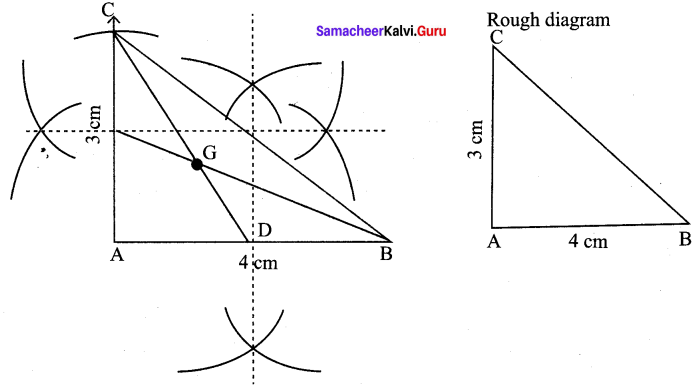
Construction:
Step 1 : Draw ∆ABC with AB = 4 cm, AC = 3 cm, ∠A = 90°
Step 2 : Draw perpendicular bisectors of any two sides (AB and AC) to find the mid points of AB and AC.
Step 3 : Draw the medians CD and BE. Let them meet at G.
Step 4 : G is the centroid of the given triangle.
9th Maths Exercise 4.5 Question 3.
Draw the ∆ABC , where AB = 6 cm, ∠B = 110° and AC = 9 cm and construct the centroid.
Solution:
In ∆ABC,
AB = 6 cm,
∠B = 110°
AC = 9 cm
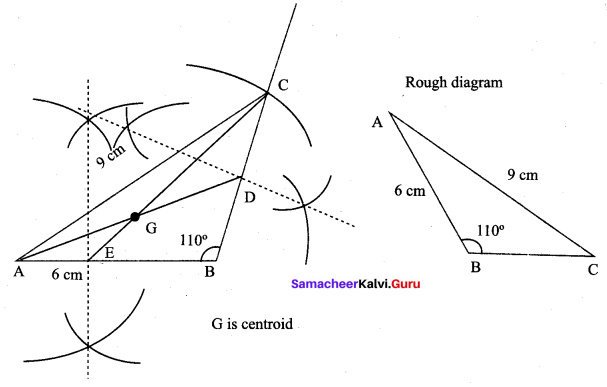
Construction:
Step 1 : Draw ∆ABC with AB = 6 cm, ∠B =110°, AC = 9 cm
Step 2 : Draw perpendicular bisectors of any two sides (BC and AB) to find the mid points of BC and AB.
Step 3 : Construct medians AD and CE. Let them meet at G.
Step 4 : G is the centroid of the given ∆ABC.
9th Geometry 4.5 Question 4.
Construct the ∆PQR such that PQ = 5 cm, PR = 6 cm and ∠QPR = 60° and locate its centroid.
Solution:
In ∆PQR, PQ = 5 cm, PR = 6 cm, ∠QPR = 60°
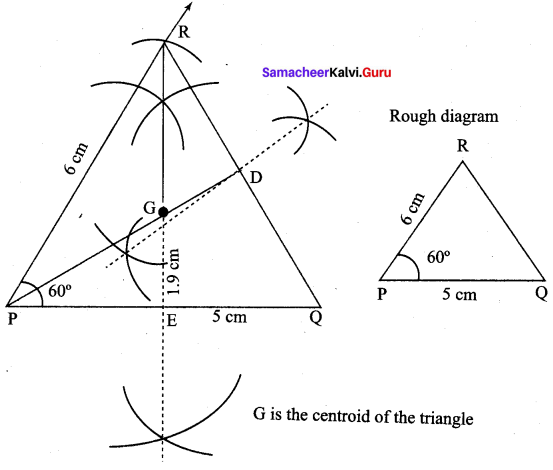
Construction :
Step 1 : Draw ∆PQR with the given measurement
Step 2 : Draw perpendicular bisectors of any two sides (PQ and QR) to find the mid points of PQ and QR.
Step 3 : Draw medians PD and RE. Let them meet at G.
Step 4 : G is the centroid of the given ∆PQR.
9th Standard Maths Exercise 4.5 Question 5.
Draw ∆PQR with sides PQ = 7 cm, QR = 8 cm and PR = 5 cm and construct its Orthocentre.
Solution:
∆PQR with sides PQ = 7 cm,
QR = 8 cm,
PR = 5 cm.
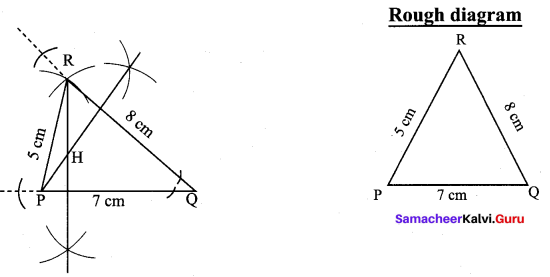
Construction:
(i) Draw the ∆PQR with the given measurements.
(ii) Construct altitudes from any two vertices (R and P) to their opposite sides (PQ and QR) respectively.
(iii) The point of intersection of the altitude H is the Orthocentre at the given ∆PQR.
Samacheer Kalvi 9th Maths Exercise 4.5 Question 6.
Draw an equilateral triangle of sides 6.5 cm and locate its Orthocentre.
![]()
Solution:
Equilateral triangle at sides 6.5 cm.
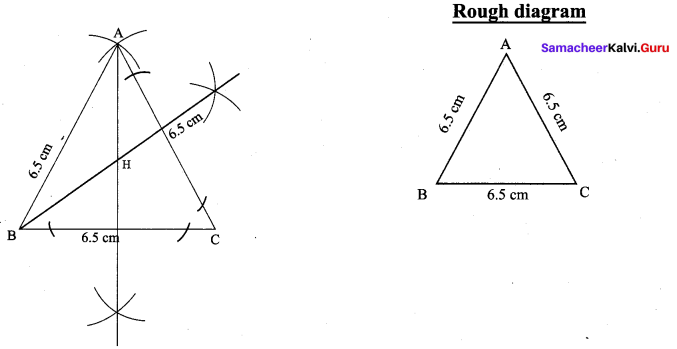
Construction :
(i) Draw the ∆ABC with the given measurements.
(ii) Construct altitudes from any two vertices A and B, to their opposite sides BC and AC respectively.
(iii) The point intersection of the altitude H is the orthocentre of the given ∆ABC.
9th Maths Geometry Exercise 4.5 Solutions Question 7.
Draw ∆ABC, where AB = 6 cm, ∠B = 110° and BC = 5 cm and construct its Orthocentre.
Solution:
∆ABC, where AB = 6 cm,
B = 110° and
BC = 5 cm.
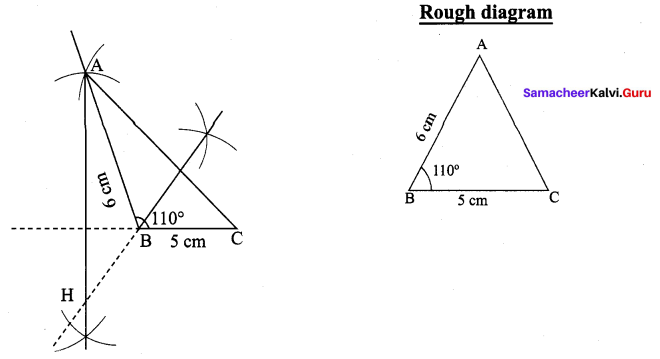
(i) Draw the ∆ABC with the given measurements.
(ii) Construct altitudes from any two vertices (A and B), to their opposite sides (BC and AC) respectively.
(iii) The point of intersection the altitude H is the orthocentre of the given ∆ABC.
9th Standard Maths Geometry Exercise 4.5 Question 8.
Draw and locate the Orthocentre of a right triangle PQR where PQ = 4.5 cm, QR = 6 cm and PR = 7.5 cm.
Solution:
Right triangle PQR where PQ = 4.5 cm, QR = 6 cm and PR = 7.5 cm.
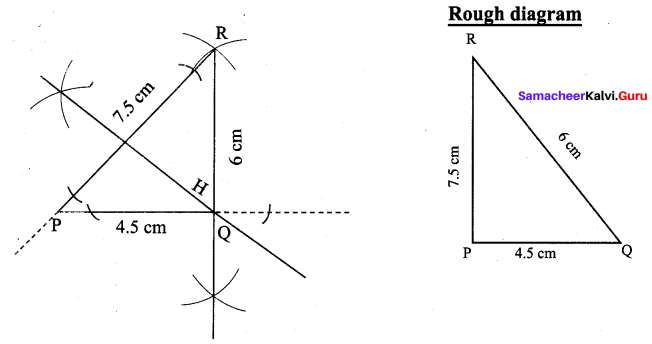
Construction:
(i) Draw the ∆PQR with the given measurements.
(ii) Construct altitudes from any two vertices R and Q, to their opposite sides PQ and PR respectively.
(iii) The point of intersection of the altitude H is the orthocentre of the given ∆PQR.