Students can Download Maths Chapter 2 Measurements Ex 2.1 Questions and Answers, Notes Pdf, Samacheer Kalvi 8th Maths Book Solutions Guide Pdf helps you to revise the complete Tamilnadu State Board New Syllabus and score more marks in your examinations.
Tamilnadu Samacheer Kalvi 8th Maths Solutions Term 1 Chapter 2 Measurements Ex 2.1
8th Maths Exercise 2.1 Question 1.
Fill in the blanks:
(i) The ratio between the circumference and diameter of any circle is _________.
(ii) A line segment which joins any two points on a circle is a ______.
(iii) The longest chord of a circle is _______.
(iv) The radius of a circle of diameter 24 cm is ______.
(v) A part of circumference of a circle is called as _____.
Solution:
(i) π
(ii) chord
(iii) diameter
(iv) 12 cm
(v) an arc
Samacheer Kalvi 8th Maths Book Solutions Question 2.
Match the following

Solution:
(i) 3
(ii) 4
(iii) 5
(iv) 2
(v) 1
Class 8 Maths Exercise 2.1 Solution Question 3.
Find the central angle of the shaded sectors (each circle is divided into equal sectors)
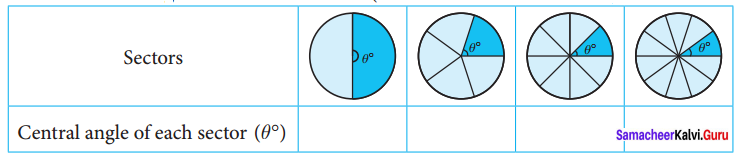
Solution:
8th Maths 2.1 Question 4.
For the sectors with given measures, find the length of the arc, area and perimeter, (π = 3.14)
(i) central angle 45°, r = 16 cm
(ii) central angle 120°, d = 12.6 cm
(iii) central angle 60°, r = 36 cm
(iv) central angle 72°, d = 10 cm
Solution:
(i) Central angle 45°, r = 16 cm
Length of the arc l = \(\frac{\theta^{\circ}}{360^{\circ}}\) × 2πr units
l = \(\frac{45^{\circ}}{360^{\circ}}\) × 2 × 3.14 × 16 cm
l = \(\frac{1}{8}\) × 2 × 3.14 × 16 cm
l = 12.56 cm
Area of the sector = \(\frac{\theta^{\circ}}{360^{\circ}}\) × πr2
A = \(\frac{45^{\circ}}{360^{\circ}}\) × 3.14 × 16 × 16
A = 100.48 cm2
Perimeter of the sector
P = l + 2r units
P = 12.56 + 2(16) cm
P = 44.56 cm
(ii) Central angle 120°, d = 12.6 cm
∴ r = \(\frac{12.6}{2}\) cm
r = 6.3 cm
Length of the arc


Area of the sector missing
Perimeter of the sector
P = l + 2r units
P = 6.28 + 2(5) cm
P = 6.28 + 10 cm
P = 16.28 cm
Question 5.
From the measures given below, find the area of the sectors.
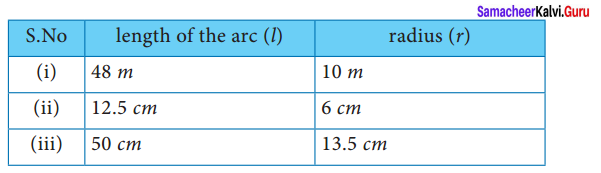
Solution:
(i) Area of the sector
A = \(\frac{l r}{2}\) sq. units
l = 48 m
r = 10 m
= \(\frac{48 \times 10}{2}\) m2
= 24 × 10 m2
= 240 m2
Area of the sector = 240 m2
(ii) length of the arc l = 12.5 cm
Radius r = 6 cm
Area of the sector
A = \(\frac{l r}{2}\) sq. units
= \(\frac{12.5 \times 6}{2}\)
= 12.5 × 3 cm2 cm2
= 37.5 cm2
Area of the sector = 37.5 cm2
(iii) length of the arc l = 50 cm
Radius r = 13.5 cm
Area of the sector
A = \(\frac{l r}{2}\) sq. units
= \(\frac{50 \times 13.5}{2}\)
= 25 × 13.5 cm2 cm2
= 337.5 cm2
Area of the sector = 337.5 cm2
Question 6.
Find the central angle of each of the sectors whose measures are given below (π = \(\frac{22}{7}\))
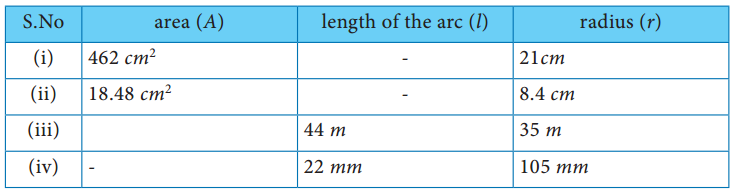
Solution:
(i) Radius of the sector = 21 cm
Area of the sector = 462 cm2
\(\frac{l r}{2}\) = 462
\(\frac{l \times 21}{2}\) = 462

∴ Central angle of the sector = 120°
(ii) Radius of the sector = 8.4 cm
Area of the sector = 18.48 cm2

(iii) Radius of the sector = 35 m
Length of the arc l = 44 m

Question 7.
Answer the following questions:
(i) A circle of radius 120 m is divided into 8 equal sectors. Find the length of the arc of each of the sectors.
(ii) A circle of radius 70 cm is divided into 5 equal sectors. Find the area of each of the sectors.
Solution:
(i) Radius of the circle r = 120 m
Number of equal sectors = 8

(ii) Radius of the sector r = 70 cm
Number of equal sectors = 5
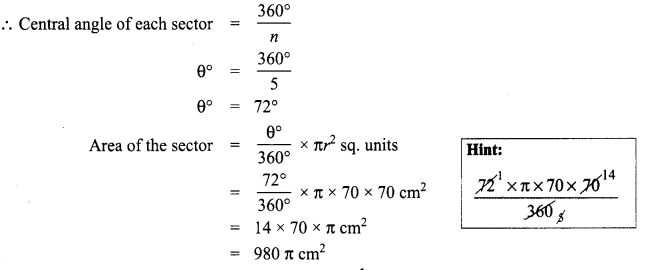
Note: We can solve this problem using A = \(\frac{1}{n}\) πr2 sq. units also.
Question 8.
Find the area of a sector whose length of the arc is 50 mm and radius is 14 mm.
Solution:
Length of the arc of the sector l = 50 mm
Radius r = 14 mm
Area of the sector = \(\frac{l r}{2}\) sq. units = \(\frac{50 \times 14}{2}\) mm2 = 50 × 7 mm2 = 350 mm2
Area of the sector = 350 mm2
Question 9.
Find the area of a sector whose perimeter is 64 cm and length of the arc is 44 cm.
Solution:
Length of the arc of the sector l = 44 cm
Perimeter of the sector P = 64 cm
l + 2r = 64 cm
44 + 2 r = 64 .
2 r = 64 – 44
2 r = 20
r = \(\frac{20}{2}\) = 10 cm2
Area of the sector = \(\frac{l r}{2}\) sq. units = \(\frac{44 \times 10}{2}\) cm2 = 22 × 10 cm2 = 220 cm2
Area of the sector = 220 cm2
Question 10.
A sector of radius 4.2 cm has an area 9.24 cm2. Find its perimeter
Solution:
Radius of the sector r = 4.2 cm
‘ Area of the sector = 9.24 cm2
\(\frac{l r}{2}\) = 9.24
\(\frac{l \times 4.2}{2}\) = 9.24
l × 2.1 = 9.24
l = \(\frac{9.24}{2.1}\)
l = 4.4 cm
Perimeter of the sector = 1 + 2r units = 4.4 + 2(4.2) cm
= 4.4 + 8.4 cm = 12. 8 cm
Perimeter of the sector = 12.8 cm
Question 11.
Infront of a house, flower plants are grown in a circular quadrant shaped pot whose radius is 2 feet. Find the area of the pot in which the plants grow. (π = 3.14)

Solution:
Central angle of the quadrant = 90°
Radius of the circle = 2 feet
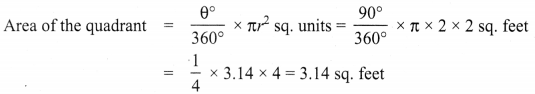
Area of the quadrant = 3.14 sq. feet (approximately)
Question 12.
Dhamu fixes a square tile of 30 cm on the floor. The tile has a sector design on it as shown in the figure. Find the area of the sector, (π = 3.14).

Solution:
Side of the square = 30 cm
∴ Radius of the sector design = 30 cm
Given design in the design of a circular quadrant.
Area of the quadrant = \(\frac{1}{4}\) πr2 sq. units
= \(\frac{1}{4}\) × 3.14 × 30 × 30 cm2
= 3.14 × 15 × 15 cm2
∴ Area of the sector design = 706.5 cm2 (approximately)
Question 13.
A circle is formed with 8 equal granite stones as shown in the figure each of radius 56 cm and whose central angle is 45°. Find the area of each of the granite. (π = \(\frac{22}{7}\))

Solution:
Number of equal sectors ‘n’ = 8
Radius of the sector ‘r’ = 56 cm
Area of the each sector = \(\frac{1}{n}\) πr2 sq. units
= \(\frac{1}{8} \times \frac{22}{7}\) × 56 × 56 cm2 = 1232 cm2
Area of each sector = 1232 cm2 (approximately)