Samacheer Kalvi 8th Maths Guide Chapter 4 வாழ்வியல் கணிதம் Ex 4.4

Tamilnadu State Board New Syllabus Samacheer Kalvi 8th Maths Guide Pdf Chapter 4 வாழ்வியல் கணிதம் Ex 4.4 Textbook Questions and Answers, Notes.

TN Board 8th Maths Solutions Chapter 4 வாழ்வியல் கணிதம் Ex 4.4

கேள்வி 1.
கோடிட்ட இடங்களை நிரப்புக.

i. A என்பவர் ஒரு வேலையை 3 நாள்களிலும் B என்பவர் 6 நாள்களிலும் முடிப்பர் எனில், இருவரும் ஒன்றாகச் சேர்ந்து அந்த வேலையை ………. நாள்களில் முடிப்பர்.
விடை:
25

ii. 5 நபர்கள் 5 வேலைகளை 5 நாள்களில் செய்து முடிப்பர் எனில், 50 நபர்கள் 50 வேலைகளை …………….. நாள்களில் செய்து முடிப்பர். A என்பவர் ஒரு வேலையை 24 நாள்களில் முடிப்பார்.
விடை:
2

iii. A மற்றும் B ஆகியோர் ஒன்றாக இணைந்து ஒரு வேலையை 6 நாள்களில் முடிப்பர் எனில், B என்பவர் தனியே அந்த வேலையை ……………… நாள்களில் முடிப்பார்.
விடை:
8

iv. A என்பவர் தனியே ஒரு வேலையை 35 நாள்களில் முடிப்பார். B ஆனவர், A ஐ விட 40% கூடுதல் திறன் வாய்ந்த வர் எனில், B ஆனவர் அந்த வேலையை ………… நாள்களில் முடிப்பார்.
விடை:
5

v. A என்பவர் தனியே ஒரு வேலையை 10 நாள்களிலும் B ஆனவர் ₹1,20,000 தனியே 15 நாள்களிலும் முடிப்பர். அவர்கள் இந்த வேலையை ₹200000 தொகைக்கு ஒப்புக் கொண்டனர் எனில், A பெறும் தொகை
…… ஆகும்.
விடை:
₹1,20,000

கேள்வி 2.
210 ஆண்கள் நாளொன்றுக்கு 12 மணி நேரம் வேலை செய்து ஒரு வேலையை 18 நாள்களில் முடிப்பர். அதே வேலையை நாளொன்றுக்கு 14 மணி நேரம் வேலை செய்து, 20 நாள்களில் முடிக்க எத்தனை ஆண்கள் தேவை?
தீர்வு :

P₁ = 210, D₁ = 18, H₁ = 12, W₁ = 1
P₂ = x, D₂ = 20, H₂ = 14, W₂ = 1
சூத்திர முறை :

x = 9 x 18
x = 162

கேள்வி 3.
ஒரு சிமிட்டி தொழிற்சாலையானது, 36 இயந்திரங்களின் உதவியுடன் 12 நாள்களில் 7000 சிமிட்டி பைகளைத் தயாரிக்கிறது. 24 இயந்திரங்களைப் பயன்படுத்தி, 18 நாள்களில் எத்தனை சிமிட்டி பைகளைத் தயாரிக்கலாம்? தீர்வு :

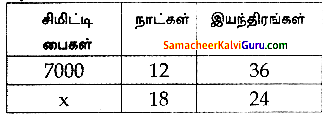
C₁ = 7000, D₁ = 12, M₁ = 36, W₁ = 1
C₂ = x , D₂ = 18, M₂ = 2
சூத்திர முறை :


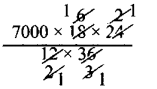
x = 7000 சிமிட்டி பைகளைத்
7000 சிமிட்டி பைகளைத் தயாரிக்கலாம்

கேள்வி 4.
ஒரு சோப்புத் தொழிற்சாலையானது, நாளொன்றுக்கு 15 மணி நேரம் வேலை செய்து 6 நாள்களில் 9600 சோப்புகளைத் தயாரிக்கிறது. நாளொன்றுக்கு கூடுதலாக 3 மணி நேரம் வேலை செய்து 14400 சோப்புகள் தயாரிக்க அதற்கு எத்தனை நாள்கள் ஆகும்?
தீர்வு :

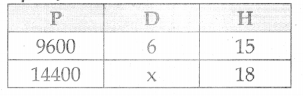
படி 1: அதிக தயாரிப்புக்கு அதிக நாட்கள் தேவை. எனவே நேர்மாறல் ஆகும்.
பெருக்கல் காரணி \(\frac{14400}{9600}\)

படி 2 : குறைவான நேரத்திற்கு அதிகநாள் தேவைப்படும். காவே எதிர்மாறல் ஆகும்.
பெருக்கல் காரணி \(\frac{15}{18}\)

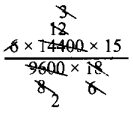
x = 15 நாட்கள்

கேள்வி 5.
6 சரக்கு வண்டிகள் நாள்களில் 135 டன்கள் சரக்குகளை இடம் பெயர்க்கின்றன எனில், 1800 டன்கள் சரக்குகளை 4 நாள்களில் இடம் பொர்ர்க எதனை சரக்கு வண்டிகள் கூடுதலாகத் தேவை ?

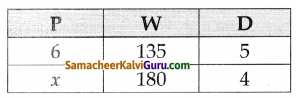
P₁ = 6
D₁ = 5
W₁ = 135
P₂ = x
D₂ = 4
W₂ = 180
சூத்திர முறை :

x = 10
கூடுதலாக 4 சரக்கு வண்டிகள் தேவை

கேள்வி 6.
A என்பவர் ஒரு வேலையை 12 மணி நேரத்தில் முடிப்பார். B மற்றும் C அந்த வேலையை 3 மணி நேரத்திலும், A மற்றும் C அந்த வேலையை 6 மணி நேரத்திலும் செய்து முடிப்பர். அதே வேலையை B தனியே எவ்வளவு மணி நேரத்தில் முடிப்பர்?
தீர்வு :
மொத்த வேலை = மீசிம (3,6,12) = 12 அலகு
A செய்த வேலை \(\frac { 12 }{ 12 }\) = 1 அலகு/மணி
A + C முடித்தது = \(\frac { 12 }{ 6 }\) = 2 அலகு/மணி
C முடித்தது = 2 – 1 = 1 அலகு/மணி
B + C முடித்தது = \(\frac { 12 }{ 3 }\) = 4 அலகு/மணி
B = 4 – 1 = 3 அலகு/மணி
B மட்டும் தனியே முடித்த வேலை \(\frac { 12 }{ 3 }\) = 4 மணி

கேள்வி 7.
A மற்றும் B ஆகியோர் ஒரு வேலையை 12 நாள்களிலும், B மற்றும் C ஆகியோர் அதை 15 நாள்களிலும் A மற்றும் C ஆகியோர் அதை 20 நாள்களிலும் முடிப்பர். ஒவ்வொருவரும் தனித்தனியே அந்த வேலையை எத்தனை நாள்களில் முடிப்பர்?
தீர்வு :
மொத்த வேலை = மீசிம (12,15,20) = 60
A + B முடித்த வேலை = \(\frac { 60 }{ 12 }\) = 5
B+C முடித்த வேலை
= \(\frac { 60 }{ 15 }\) = 4

மீசிம் = 3 x 4 x 5
A + C முடித்த வேலை
= \(\frac { 60 }{ 20 }\) = 3
= 60
A + B = 5 —— (1)
B + C = 4 ————- (2)
A + C = 3 ————- (3)
(1) x (2) ஐ தீர்க்க

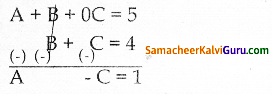
A – C = 1 — —– (4)
(3) & (4) ஐ தீர்க்க

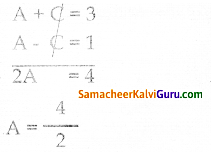
A = 2 என (1) ல் பிரதியிட
A + B = 5
B = 5 – 2
B = 3
B = 3 என (2)ல் பிரதியிட
B + C = 4
C = 4 – 3
C = 1
A மட்டும் தனியே செய்த வேலை \(\frac { 60 }{ 2 }\) = 30 நாட்கள்
B மட்டும் தனியே செய்த வேலை \(\frac { 60 }{ 3 }\) = 20 நாட்கள்
60 மட்டும் தனியே செய்தவேலை \(\frac { 60 }{ 1 }\) = 60 நாட்கள்.

கேள்வி 8.
தச்சர் A ஆனவர் ஒரு நாற்காலியின் பாகங்களைப் பொருத்த 15 நிமிடங்கள் எடுத்துக் கொள்கிறார். அதே வேலையைச் செய்ய தச்சர் B ஆனவர் தச்சர் A ஐ விட 3 நிமிடங்கள் கூடுதலாக எடுத்துக் கொள்கிறார். இருவரும் இணைந்து வேலைச் செய்து 22 நாற்காலிகளின் பாகங்களைப் பொருத்த எவ்வளவு நேரமாகும்?
தீர்வு :
A ஆனவர் 15 நிமிடங்களில் செய்த வேலை= \(\frac { 1 }{ 15 }\)
B ஆனவர் A ஐ விட 3 நிமிடங்கள் கூடுதலாக செய்த வேலை = \(\frac { 1 }{ 18 }\)
18 இருவரும் சேர்ந்து செய்த வேலை

இருவரும் இணைந்து 22 நாற்காலிகளின் பாகங்களை பொருத்து ஆகும் நேரம்.

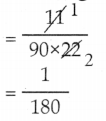
இருவரும் இணைந்து செய்ய ஆகும் நேரம் = 180 நிமிடங்கள்/3 மணி.

கேள்வி 9.
A ஆனவர் ஒரு வேலையை 45 நாள்களில் முடிப்பார். அவர் 15 நாள்கள் மட்டுமே வேலையைச் செய்கிறார். மீதமுள்ள வேலையை B ஆனவர் 24 நாள்களில் முடிக்கிறார். எனில், அந்த வேலையின் 80% ஐ இருவரும் இணைந்து முடிக்க ஆகும் நேரத்தைக் காண்க.
தீர்வு:
ஒரு நாளில் A செய்த வேலை = \(\frac{1}{45} \times 15=\frac{1}{3}\)
\(\frac { 2 }{ 3 }\) மடங்கு வேலையை B ஆனவர் 24 நாட்களில் முடிக்கிறார்.
B ஒரு நாளில் செய்த வேலை = 24 x \(\frac { 3 }{ 2 }\) = 36 நாட்கள்
இருவரும் இணைந்து

80% வேலையை முடிக்க ஆகும் நேரம்
= \(\frac{1}{20} \times \frac{100}{80}\)
= \(\frac{1}{16}\)
= 16 நாட்கள்

கேள்வி 10.
A என்பவர் B என்பவரைக் காட்டிலும் வேலை செய்வதில் மூன்று மடங்கு வேகமானவர். B ஆனவர் ஒரு வேலையை 24 நாள்களில் முடிப்பார் எனில், இருவரும் இணைந்து அந்த வேலையை முடிக்க எத்தனை நாள்கள் எடுத்துக் கொள்வர் எனக் காண்க.
தீர்வு :
B செய்த வேலை = \(\frac { 1 }{ 24 }\)
A செய்த வேலை 3 x \(\frac { 1 }{ 24 }\) = \(\frac { 1 }{ 8 }\)
இருவரும் இணைந்து

இருவரும் இணைந்து 6 நாட்களில் செய்து முடிப்பர்.