Tamilnadu State Board New Syllabus Samacheer Kalvi 8th Maths Guide Pdf Chapter 3 இயற்கணிதம் Ex 3.7 Textbook Questions and Answers, Notes.
TN Board 8th Maths Solutions Chapter 3 இயற்கணிதம் Ex 3.7
கேள்வி 1.
கோடிட்ட இடங்களை நிரப்புக
i) ax + b = 0 என்ற சமன்பாட்டின் தீர்வு ஆகும்.
விடை :
x = \(\frac{-b}{a}\)
ii) a மற்றும் b மிகை முழுக்கள் எனில் ax = b என்ற சமன்பாட்டின் தீர்வு எப்பொழுதும், ஆகும்.
விடை :
x = \(\frac{b}{a}\) (அ) நேர்மறை
![]()
iii) ஓர் எண்ணிலிருந்து அதன் ஆறில் ஒரு பங்கைக் கழித்தால் 25 கிடைக்கிறது எனில், அவ்வெண் …………………. ஆகும்.
விடை :
x = 30
iv) ஒரு முக்கோணத்தின் கோணங்கள் 2:3:4 என்ற விகிதத்தில் அமைந்துள்ளது எனில், அம்முக்கோணத்தின் பெரிய கோணத்திற்கும், சிறிய கோணத்திற்கும் உள்ள வித்தியாசம் ஆகும்.
விடை :
40°
v) a + b = 23 என்ற சமன்பாட்டில் a இன் மதிப்பு 14 எனில், b இன் மதிப்பு ………………. ஆகும்.
விடை :
9
![]()
II. சரியா தவறா எனக் கூறுக
i) ஓர் எண் மற்றும் அதன் இருமடங்கு இவற்றின் கூடுதல் 48, இதனை y + 2y = 48 என எழுதலாம்.
விடை :
சரி
ii) 5(3x + 2) = 3(5x – 7) என்ப து ஒரு மாறியில் அமைந்த ஒருபடிச் சமன்பாடு ஆகும்.
விடை :
தவறு
iii) ஓர் எண்ணின் மூன்றில் ஒரு மடங்கு என்பது அவ்வெண்ணிலிருந்து 10 ஐக் கழிப்பதற்குச் சமம் எனில், அந்த சமன்பாட்டின் தீர்வு x = 25 ஆகும்.
விடை :
சரி
கேள்வி 3.
ஓர் எண் மற்றோர் எண்ணின் 7 மடங்கு ஆகும். அவற்றின் வித்தியாசம் 18 எனில், அவ்வெண்களைக் காண்க. தீர்வு :
ஒரு எண் x என்க.
மற்றொரு எண் 1 என்க.
x = 71 —————-(1)
x – y = 18 —————-(2)
⇒ 7y – y = 18 (1) லிருந்து
6y = 18
y = 18/6
y = 3
y = 3 என (1) ல் பிரதியிட
x = 7 (3)
x = 21
![]()
கேள்வி 4.
அடுத்தடுத்த மூன்று ஒற்றை எண்களின் கூடுதல் 75 எனில், அவற்றுள் எது பெரிய எண்?
தீர்வு :
ஒற்றை எண்ணை x என்க .
அடுத்தடுத்த மூன்று ஒற்றை எண்கள் x, x+2, x+4 ஆகும்.
கூடுதல் 75
x + ( x + 2) + (x + 4) = 75
3x + 6 = 75
3x = 75 – 6
3x = 69
x = 69/3
x = 23
மூன்று எண்கள் 23, 25, 27
பெரிய எண் 27 ஆகும்.
கேள்வி 5.
ஒரு செவ்வகத்தின் நீளமானது அதன் அகலத்தின் மூன்றில் ஒரு பங்கு ஆகும். அச்செவ்வகத்தின் சுற்றளவு 64மீ எனில், செவ்வகத்தின் நீளம் மற்றும் அகலத்தைக் காண்க.
தீர்வு :
அகலம் x என்க
நீளம் = \(\frac{1}{3}\) x b
செவ்வகத்தின் சுற்றளவு = 2(l + b) அலகுகள்
2(l + b) = 64
2(\(\frac{\mathrm{b}}{3}\) + b) = 64
\(\frac{b+3 b}{3}=\frac{64}{2}\)
\(\frac{4 b}{3}=32\)
b = \(\frac{32 \times 3}{4}\)
b = 24m
∴ நீளம் = \(\frac{b}{3}=\frac{24}{3}\) = 8மீ
∴ நீளம் = 8மீ, அகலம் = 24 மீ
![]()
கேள்வி 6.
₹ 5 மற்றும் ₹10 மதிப்புகளை மட்டுமே கொண்ட 90 பணத்தாள்கள் உள்ளன. அதன் மதிப்பு ₹ 500 எனில், ஒவ்வொரு முக மதிப்புடைய பணத்தாளும் எத்தனை உள்ளன எனக் காண்க.
தீர்வு :
x என்பது Rs. 5 ன் எண்ணிக்கை .
y என்பது Rs. 10 ன் எண்ணிக்கை .
x+y = 90 — (1)
5x + 10y = 500 —— (2)
1& 2 ஐ தீர்க்க
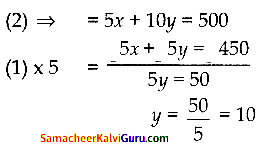
y = 10
y = 10 என (1)ல் பிரதியிட
x + y = 90
x + 10 = 90
x = 90 – 10 = 80
x = 80
கேள்வி 7.
தேன்மொழியின் தற்போதைய வயது முரளியின் வயதைவிட 5 ஆண்டுகள் அதிகம் ஆகும். 5 ஆண்டுகளுக்கு முன் தேன்மொழிக்கும் முரளிக்கும் இடையே இருந்த வயது விகிதம் 3:2 எனில், அவர்களின் தற்போதைய வயது என்ன?
தீர்வு :
x என்பது தேன்மொழியின் வயது என்க.
y என்பது முரளியின் வயது என்க.
x = y + 5
x – y = 5 — —————– (1)
\(\frac{x-5}{y-5}=\frac{3}{2}\)
2(x-5) = 3(1-5)
2x – 10 = 3y – 15
2x – 3y = -15 + 15 = -5
2x – 31 = -5 ——- ———(2)
1 & 2 ஐ தீர்க்க
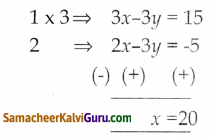
x = 20
x = 20 என (1) ல் பிரதியிட
20 – 1 = 5
20 – 5 = y
y = 15
தேன்மொழியின் வயது = 20
முரளியின் வயது = 15
![]()
கேள்வி 8.
இரண்டு இலக்கங்களைக் கொண்ட ஓர் எண்ணின் இலக்கங்களின் கூடுதல் 9. அந்த எண்ணிலிருந்து 27 ஐக் கழிக்க அவ்வெண்களின் இலக்கங்கள் இடம் மாறிவிடும் எனில், அவ்வெண்ணைக் காண்க.
தீர்வு :
x என்பது 10 ம் இலக்கம் என்க.
y என்பது ஒன்றாம் இலக்கம் என்க.
∴ அந்த எண் 10x + y
இடம் மாறிய எண் 10 y + x
x + y = 9 ——(1)
10x + y – 27 = 10y +x
10x – x + y -101 = 27
9x – 9y = 27
÷ 9 x – y = 3 ————–(2)
(1) & (2) ஐ தீர்க்க.
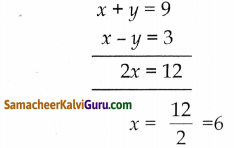
x = 6
x = 6 என (1) ல் பிரதியிட
x + y = 9
6 + y = 9
y = 9 – 6
y = 3
அந்த எண் 63.
கேள்வி 9.
ஒரு பின்னத்தின் பகுதியானது தொகுதியை விட 8 அதிகம் ஆகும். அப்பின்னத்தில் தொகுதியின் மதிப்பு 17 அதிகரித்து பகுதியின் மதிப்பு 1 ஐக் குறைத்தால் \(\frac{3}{2}\) என்ற பின்னம் கிடைக்கிறது எனில், முதலில் எடுத்துக் கொண்ட உண்மையான பின்னம் யாது?
தீர்வு :
x என்பது பின்னத்தின் தொகுதி என்க.
∴ பகுதி x + 8 ஆகும்.
பின்ன = \(\frac{x}{x+8}\)
\(\frac{(x+17)}{(x+8-1)}=\frac{3}{2}\)
\(\frac{x+17}{x+7}=\frac{3}{2}\)
2(x + 17) = 3(x+7)
2x + 34 = 3x +21
3x -2x = 34 – 21
x = 13
∴ பின்னம் எண் = \(\frac{x}{x+8}\)
= \(\frac{13}{21}\)
![]()
கேள்வி 10.
ஒரு தொடர்வண்டி மணிக்கு 60 கி.மீ வேகத்தில் சென்றால் சேர வேண்டிய இடத்திற்கு 15 நிமிடங்கள் தாமதமாக சென்று சேரும். ஆனால் அவ்வண்டி மணிக்கு 85 கி.மீ வேகத்தில் சென்றால் சேர வேண்டிய இடத்திற்கு 4 நிமிடங்கள் மட்டுமே தாமதமாக சென்று சேரும் எனில், அத்தொடர்வண்டி கடக்க வேண்டிய பயணத் தூரத்தைக் காண்க.
தீர்வு :
பயண நேரத்தை x என்க.

12(60 T + 15) = 17(60T – 4)
720 T + 180 = 1020 T – 68
1020 T – 720 T = 180 + 68
300 T = 248
T = \(\frac{248}{300}\) மணி
தூரம் = நேரம் x வேகம்
= \(\frac{248}{300}\) x 60 = 49.6கி.மீ
ஆகும்.
ஆகும்.
அ) 620
ஈ) 680
கொள்குறிவகை வினாக்கள்
கேள்வி 11.
ஓர் எண் மற்றும் அதன் பாதியின் கூடுதல் 30 எனில் அவ்வெண்
அ) 15
ஆ) 20
இ) 25
ஈ) 40
விடை :
(ஆ) 20
![]()
கேள்வி 12.
ஒரு முக்கோணத்தின் வெளிக்கோணம் 120°, அதன் ஓர் உள்ளெதிர்க் கோணம் 58° எனில், மற்றோர் உள்ளெதிர்க் கோணம் ………………… ஆகும்.
ஆ) 720
இ) 780
விடை :
(அ) 62°
கேள்வி 13.
ஆண்டிற்கு 5% வட்டி வீதத்தில் ஓர் ஆண்டிற்கு ₹.500 ஐத் தனி வட்டியாகத் தரும் அசல் எவ்வளவு?
அ) 50000
ஆ) 30000
இ) 10000
ஈ) 5000
விடை :
(இ) 10000
கேள்வி 14.
இரண்டு எண்களின் மீ.சி.ம மற்றும் மீ.பொ.கா ஆகியவற்றின் பெருக்குத் தொகை 24 ஆகும். அவற்றுள் ஓர் எண் 6 எனில், மற்றோர் எண் …………………. ஆகும்.
அ) 6
ஆ) 2
இ) 4
ஈ) 8
விடை :
(இ) 4
![]()
கேள்வி 15.
அடுத்தடுத்த முன்று எண்களில் மிகப்பெரிய எண் x + 1, எனில் மிகச்சிறிய எண் ………………….ஆகும்.
அ) x
ஆ) x+1
இ) x+2
ஈ) x-1
விடை :
(ஈ) x-1