Students can Download Maths Chapter 1 Number System Intext Questions and Answers, Notes Pdf, Samacheer Kalvi 7th Maths Book Solutions Guide Pdf helps you to revise the complete Tamilnadu State Board New Syllabus and score more marks in your examinations.
Tamilnadu Samacheer Kalvi 7th Maths Solutions Term 1 Chapter 1 Number System Intext Questions
(Try These Textbook Page No. 1)
Samacheer Kalvi 7th Maths Book Answers Question 1.
Write the following integers in ascending order: -5,0,2,4, -6,10, -10
Solution:
Plotting the points on the number line, we get

The numbers are placed in an increasing order from left to right.
∴ Ascending order: -10 < -6 < -5 < 0 < 2 < 4 < 10
7th Maths Number System Question 2.
If the integers -15, 12, -17, 5, -1, -5, 6 are marked on the number line then the integer on the extreme left is _____ .
Solution:
The least number will be on the extreme left.
∴ -17 will be on the extreme left.
Number System 7th Standard Question 3.
Complete the following pattern:
50, ___ 30, 20, _, 0, -10, _, _, -40, _, ___.
Solution:
The difference between the consecutive number is 10.
50, 40, 30,20, 10, 0, -10, -20, -30, -40, -50, -60
Samacheer Kalvi 7th Maths Books Answers Question 4.
Compare the given numbers and write “<”, “>” or in the boxes.
![]()
Solution:
(a) ![]() A positive number is greater than a negative number.
A positive number is greater than a negative number.
(b) ![]() 1000,0 is less than all positive integers.
1000,0 is less than all positive integers.
(c) ![]()
7th Maths Exercise 1.1 Samacheer Kalvi Question 5.
Write the given integers in descending order, -27, 19, 0, 12, -4, -22, 47, 3, -9, -35.
Solution:
Separating positive and the negative integers, we get -27, -4, -22, -9, -35
Arranging the numbers in descending order -4 > -9 > -22 > -27 > -35
The positive numbers are 19,12,47, 3
Arranging in descending order, we get 47 > 19 > 12 > 3
0 stands in the middle.
∴ Descending order: 47 > 19 > 12 > 3 > 0 > -4 > -9 > -22 > -27 > -35
(Try This Text Book Page No. 3)
7th Maths Guide Try These Question 1.
Find the value of the following using the number line activity.
(i) (-4) + (+3)
(ii) (-4) + (-3)
(iii) (+4) + (-3)
Solution:
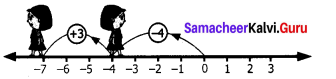
(i) (-4) + (+3)
To find the sum of (-4) and (+3), we start at zero facing positive direction continuing in the same direction and move 4 units backward to represent (-4).
Since the operation is addition we maintain the same direction and move three units forward to represent (+3)
We land at -1
So (-4) + (+3) = -1
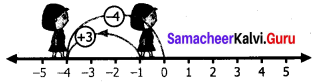
(ii) (-4) + (-3)
From zero move 4 steps backward to represent (-4)
From the same direction again move 3 units backward to represent (-3)
We land at -7 So (-4) + (-3) = -7
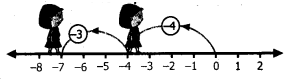
(iii) (+4) + (-3)
We start at zero facing positive direction and move 4 steps forward to represent (+4) Since the operation is addition we maintain the same direction and move three units backward to represent (-3).
We land at +1.
So (+4) + (-3) = +1
(Properties of Addition Textbook Page No. 6)
Samacheer Kalvi 7th Maths Solutions Question 1.
Complete the given table and check whether the sum of two integers is an integer or not?
(i) 7 + (-5) = (+2)
(ii) (-6)+ (-13) = (-19)
(iii) 25 + 9 = 34
(iv) (-12) + 4 = -8
(v) 41 + 32 = 73
(vi) (-19) + (-15) = (-34)
(vii) 52 + (-15) = (+37)
(viii)(-7) + 0 = (-7)
(ix) 0 + 12 = 12
(x) 14 + 0 = 14
(xi) (-6) +(-6) = (-12)
(xii) (-27) + 0 = -27
Solution:
The sum of two integers is an integer.
(Try These Textbook Page No. 7)
Samacheer Kalvi Guru 7th Maths Question 1.
Fill in the blanks:
(i) 20 + (-11) = -(11)+ 20 [∵ Addition is commutative]
(ii) (-5) + (-8) = (-8) + (-5) [∵ Addition is commutative]
(iii) (-3) +12 =12 + (-3) [∵ Addition is commutative]
7th Standard Number System Question 2.
Say True or False.
(i) (-11) + (-8) = (-8) + (-11)
(ii) -7 + 2 = 2 + (-7)
(iii) (-33) + 8 = 8 + (-33)
Solution:
(i) True, because addition is commutative for intergers
(ii) True, by commutative property on intergers
(iii) True, by commutative property on intergers
Samacheer Kalvi 7th Maths Question 3.
Verify the following.
(i) [(-2) + (-9)] + 6 = (-2) + [(-9) + 6]
(ii) [7 + (-8)] + (-5) = 7 + [(-8) + (-5)]
(iii) [(-11) + 5]+ (-14) = (-11) + [5 + (-14)]
(iv) (-5) + [(-32) +(-2)] = [(-5) + (-32) + (-2)]
Solution:
(i) [(-2) + (-9)] + 6 = (-2) + [(-9) + 6]
[(-2) + (-9)] + 6 = (-11) + 6 = -5
Also (-2) + [(-9) + 6] = (-2) + (-3) = -5
Both the cases the sum is -5.
∴ – [(-2) + (-9)] + 6 = (-2) + [(-9) + 6]
(ii) [7 + (-8)] +(-5) = 7 + [(-8) + (-5)]
Here [7 + (-8)] + (-5) = (-1) + (-5) = -6
Also 7 + [(-8) + (-5)] = 7 + (-13) = 7 – 13 = -6
In both the cases the sum is -6.
∴ [7 + (-8)] + (-5) = 7 + [(-8) + (-5)]
(iii) [(-11) + 5] + (-14) = (-11) + [5 + (-14)]
Here [(-11) + 5] + (-14) = (-6) + (-14) = (-20)
(-11) + [5 + (-14)] = (-11) +(-9) = (-20)
In both the cases the sum is -20.
∴ [(-11) + 5] + (-14) = (-11) + [5 + (-14)]
(iv) (-5) + [(-32) + (-2)] = [(-5) + (-32)] + (-2)
(-5) + [(-32) + (-2)] = (-5) + (-34) = -39
Also [(-5) + (-32)] + (-2) = (-37) + (-2) = -39
In both the cases the sum is -39.
∴ (-5)+ [(-32) +(-2)] = [(-5)+ (-32)] +(-2)
Samacheer Kalvi 7th Maths Book Answers Pdf Question 4.
Find the missing integers:
(i) 0 + (-95) = -95
(ii) -611 + 0 = -611
(iii) ____ + 0 = _____ Any integer; the same integer
(iv) 0 + (-140) = -140
Samacheer Kalvi 7th Maths Book Solutions Question 5.
Complete the following:
(i) -603 + 603 = 0
(ii) 9847+ (-9847) = 0
(iii) 1652 + (-1652) = 0
(iv) -777 + 777 = 0
(v) –5281 +5281 = 0
Exercise 1.2
Subtraction of Integers
(Try These Text book Page No. 11)
Samacheer Kalvi 7th Maths Answers Question 1.
Do the following by using number line.
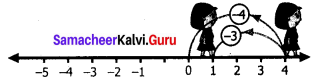
(i) (-4) – (+3)
Solution:
We start at zero facing positive direction move 4 units backward to represent (-4). Then turn towards negative side and move 3 units forward.
We reach -7.
∴ (-4) – (+3) = -7.
(ii) (-4) – (-3)
Solution:
We start at zero facing positive direction. Move 4 units backward to represent -4. Then turn towards the negative side and move 3 units backwards.
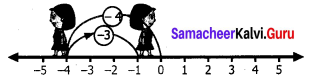
We reach at-1.
∴ (-4) – (-3) = -1.
Samacheer Kalvi Guru 7th Standard Maths Question 2.
Find the values and compare the answers.
(i) (-6) – (-2) and (-6) + 2
Solution:
(-6) – (-2) = -6 + (Additive inverse of-2)
= -6 + (+2) = -4
Also (-6)+ 2 = -4
∴ (-6) – (-2) = (-6) + 2
(ii) 35 – (-7) and 35 + 7.
Solution:
35 – (-7) = 35 + (Additive inverse of -7) = 35 + (+7) = 42
Also 35 + 7 = 42 ; 35 – (-7) =35 + 7
(iii) 26 – (+10) and 26 + (-10)
Solution:
26 – (+10) = 26 + (Additive inverse of +10) = 26 + (-10) = 16
Also 26 + (-10) = 16; 26 – (+10) = 26 + (-10)
Number System 7th Class Question 3.
Put the suitable symbol <, > or = in the boxes.
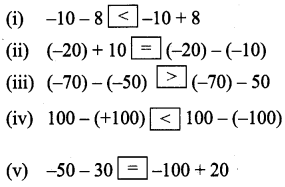
Solution:
(i) -10 – 8 = -18 & -10 + 8 = – 2
(ii) (-20) + 10 = -10 & (-20) – (-10) = -10
(iii) -70 – 50 = (-70) + (-50) = -20
(iv) 100 – (+100) = 0 & 100 – (-100) = 100 + (+100) = 200
(v) -50 – 30 = -50 + (-30) = -80 Also -100 + 20 = – 80
(Try These Text book Page No. 14)
Samacheer Kalvi Guru 7th Maths Solutions Question 1.
Fill in the blanks.
(i) (-7) – (-15) = +8
-7 – (-15) = -7 + (Additive inverse of-15)
= -7 + 15 = +8
(ii) 12 – (-7) = 19 12 – (-7) = 19
(iii) -4 – (-5) = 1
Question 2.
Find the values and compare the answers.
(i) 15 – 12 and 12 – 15
(ii) -21 – 32 and -32 – (-21)
Solution:
(i) 15 – 12 = 3 & 12-15 = 12 +(-15) = -3
![]()
(ii) -21 – 32 = (-21) + (-32) = -53
Also -32 – (-21) = (-32) + (+21) = -11 ; -53 < -11
![]()
Question 3.
Is associative property true for subtraction of integers. Take any three examples and check.
Solution:
Consider the numbers 1,2 and 3. Now (1 – 2) – 3 = -1 – 3 = -4
Also 1 – (2 – 3) = 1 – (-1) = 1 + 1 = 2
∴ (1 – 2) – ≠ 1 – (2 – 3)
∴ Associative property is not true for subtraction of integers.
Exercise 1.3
Multiplication of Integers
(Try These Textbook Page No. 16)
Question 1.
Find the product of the following
(i) (-20) × (-45) = +900 [As we know the product of two negative integers is positive, the answer is +900.]
(ii) (-9) × (-8) = 72 [ ∵ Product of two negative integers is positive]
(iii) (-30) × 40 × (-1) = (+1200) [Product of two integers with opposite sings is negative integer.
(-30) × 40 × (-1) = (-1200) × (-1) = +1200)]
(iv) (-50) × 2 × (-10) = -1000 [Product of two integers with opposite signs is negative.
(+50) × 2 × (-10) = 100 × (-10) = -1000)]
Question 2.
Complete the following table by multiplying the integers in the corresponding row and column headers.
Solution:
We know that
(i) product of two positive integers is positive
(ii) product of two negative integers is
(ii) product of two negative integers is positive
(iii) product of integers with opposite sign is negative.
∴ The table will be as follows:
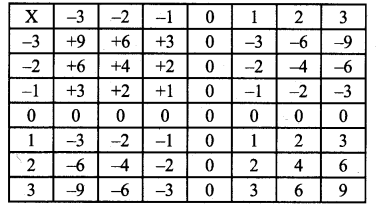
Question 3.
Which of the following is incorrect?
(i) (-55) × (-22) × (-33) < 0
(ii) (-1521) × 2511 < 0
(iii) 2512 – 1525 < 0
(iv) (1981) × (+2000) < 0
Solution:
(iii) and (iv) are incorrect because 2512 – 1252 is a positive integer.
Also (+1981) × (+2000) is a positive integer.
(Try These Textbook Page No. 18)
Question 1.
Find the product and check for equality
(i) 18 × (-5) and (-5) × 18
Solution:
Here 18 × (-5) = -90 Also (-5) × 18 = -90
∴ 18 × (-5)= (-5) × 18
(ii) 31 × (-6) and (-6) × 31
Solution:
Here 31 × (-6) = -186 Also (-6) × 31 =-186
∴ 31 × (-6)= (-6) × 31
(iii) 4 × 51 and 51 × 4
Solution:
Here 4 × 51 = 204 Also 51 × 4 = 204
∴ 4 × 51 = 51 × 4
Question 2.
Prove the following.
(i) (-20) × (13 × 4) = [(-20) × 13] × 4
Solution:
LHS = (-20) × (13 × 4) = (-20) × 52 = -1040
RHS = [(-20) × 13] × 4 = (-260) × 4 = -1040
LHS = RHS
∴ (-20) × (13 × 4) = [(-20) × 13] × 4
(ii) [(-50) × (-2)] × (-3) = (-50) × [(-2) × (-3)]
Solution:
LHS = [(-50) × (-2)] × (-3) = 100 × (-3) = -300
RHS = (-50) × [(-2) × (-3)] = (-50) × 6 =-300
LHS = RHS
∴ [(-50) × (-2)] × (-3) = (-50) × [-2) × (-3)]
(iii) [(-4) × (-3)] × (-5) = (-4) × [(-3) × (-5)]
Solution:
LHS = [(-4) × (-3)] × (-5) = 12 × (-5) = -60
RHS = (-4) × [(-3) × (-5)] = (-4) × 15 = -60
LHS = RHS
∴ [(-4) × (-3)] × (-5) = (-4) × [(-3) × (-5)]
(Try These Textbook Page No. 19)
Question 1.
Find the values of the following and check for equality:
(i) (-6) × (4 + (-5)) and ((-6) × 4) + ((-6) × (-5))
Solution:
(-6) × (4 + (-5)) = (-6) × (-1) = 6 .
((-6) × 4) + ((-6) × (-5)) = (-24)+ 30 = 6
Hence (-6) × (4 + (-5)) = ((-6) × 4) + ((-6) × (-5))
(ii) (-3) × [2 + (-8)] and [(-3) × 2] + [(-3) × 8]
Solution:
(-3) × [2 + (-8)] = (-3) × (-6) = 18
Also [(-3) × 2] + [(-3) × 8] = (-6)+ (-24) = -30
(-3) × [2 + (-8)] ≠ [(-3) × 2] + [(-3) × 8]
Question 2.
Prove the following.
(i) [(-5) × (-76)] + [(-5) × 8]
Solution:
LHS = (-5) × [(-76) + 8] = (-5) × (-68)
= +340
RHS = [(-5) × (-76)] + [(-5) × 8]
= +380 + (-40) = +380 – 40
= +340
LHS = RHS
∴ (-5) × [(-76) + 8] = [(-5) × (-76)] + [(-5) × 8]
(ii) (42 × 7) + [42 × (-3)]
Solution:
LHS = 42 × [7 + (-3)]
= 168
RHS = (42 × 7) + [42 × (-3)] = 294 – 126
= 168
LHS = RHS
∴ 42 × [7 + (-3)] = (42 × 7) + [42 × (-3)]
(iii) [(-3) × (-4)] + [(-3) × (-5)]
Solution:
LHS = (-3) × [(-4) + (-5)] = (-3) × (-9)
= +27
RHS = [(-3) × (-4)] + [(-3) × (-5)] = 12 + 15 = 27
LHS = RHS
∴ (-3) × [(-4) + (-5)] = [(-3) × (-4)] + [(-3) × (-5)]
(iv) 103 × 25 = (100 + 3) × 25 = (100 × 25) + (3 × 25)
Solution:
First consider 103 × 25 = 2575
Now (100 + 3) × 25 = 103 × 25 = 2575
Also (100 × 25) + (3 × 25) = 2500 + 75
= 2575
∴ All the three are same. 103 × 25 = (100 + 3) × 25 = (100 × 25) +(3 × 25)
Exercise 1.4
Division of Integers
(Try These Text book Page No. 22)
Question 1.
(i) (-32) ÷ 4 = _____
(ii) (-50) ÷ 50 = ____
(iii) 30 ÷ 15 = ______
(iv) -200 ÷ 10 = _____
(v) -48 ÷ 6 = ______
Solution:
(i) -8
(ii) -1
(iii) 2
(iv) -20
(v) -8