You can Download Samacheer Kalvi 12th Maths Book Solutions Guide Pdf, Tamilnadu State Board help you to revise the complete Syllabus and score more marks in your examinations.
Tamilnadu Samacheer Kalvi 12th Maths Solutions Chapter 9 Applications of Integration Ex 9.10
Choose the correct or the most suitable answer from the given four alternatives:
Question 1.
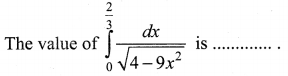
![]()
Solution:
(a) \(\frac{\pi}{6}\)
Hint:
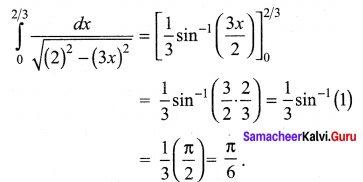
Question 2.
![]()

Solution:
(c) \(\frac{5}{2}\)
Hint:
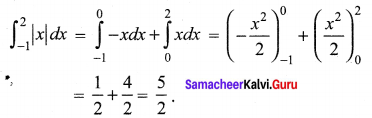
![]()
Question 3.
![]()
![]()
Solution:
(c) 0
Hint:

Question 4.
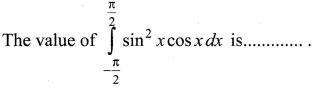

Solution:
(d) \(\frac{2}{3}\)
Hint:
It is an even function
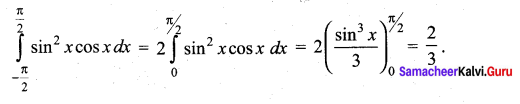
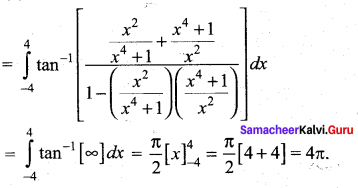
Question 5.
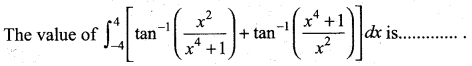
(b) 2π
(c) 3π
(d) 4π
Solution:
(d) 4π
Hint:
Question 6.
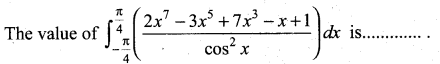
(a) 4
(b) 3
(c) 2
(d) 0
Solution:
(c) 2
Hint:

![]()
Question 7.
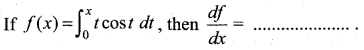
(a) cos x – x sin x
(b) sin x + x cos x
(c) x cos x
(d) x sin x
Solution:
(c) x cos x
Hint:
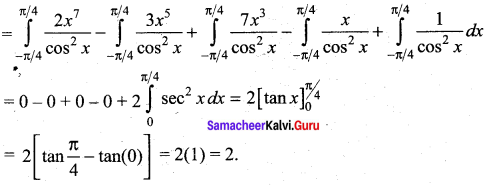
Question 8.
The area between y2 = 4x and its latus rectum is ………
![]()
Solution:
(c) \(\frac{8}{3}\)
Hint:
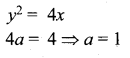
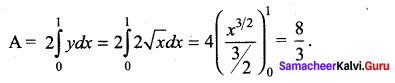
Question 9.
![]()

Solution:
(b) \(\frac{1}{10100}\)
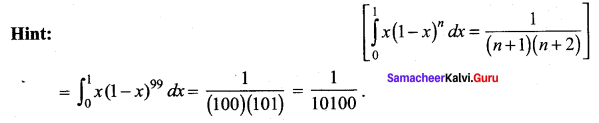
Question 10.
![]()

Solution:
(a) \(\frac{\pi}{2}\)
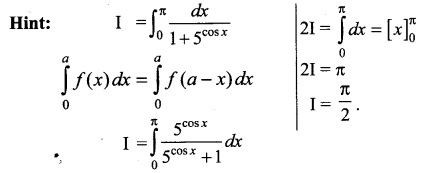
![]()
Question 11.
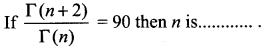
(a) 10
(b) 5
(c) 8
(d) 9
Solution:
(d) 9
Hint:

Question 12.
![]()

Solution:
(b) \(\frac{2}{9}\)
Hint:
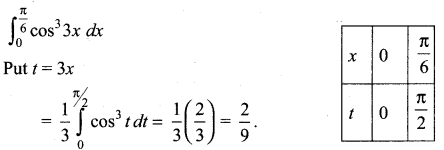
Question 13.
![]()
![]()
Solution:
\(\frac{3 \pi}{8}\)
Hint:
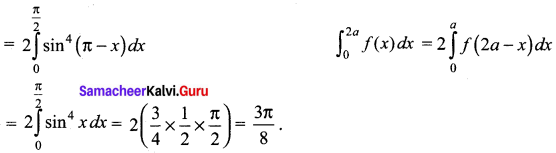
Question 14.
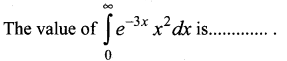
![]()
Solution:
(d) \(\frac{2}{27}\)
Hint:

![]()
Question 15.
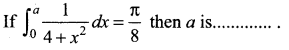
(a) 4
(b) 1
(c) 3
(d) 2
Solution:
(d) 2
Hint:

Question 16.
The volume of solid of revolution of the region bounded by y2 = x(a – x) about x-axis is ……..

Solution:
(d) \(\frac{\pi a^{3}}{6}\)
Hint:
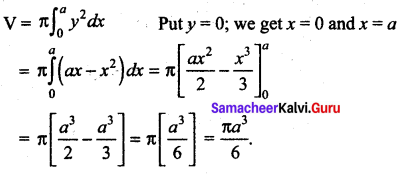
Question 17.
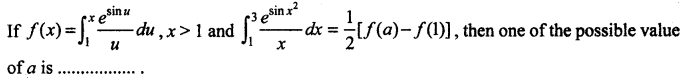
(a) 3
(b) 6
(c) 9
(d) 5
Solution:
(c) 9
Hint:

Question 18.
![]()

Solution:
(d) \(\frac{\pi^{2}}{4}-2\)
Hint:

Question 19.
![]()

Solution:
(b) \(\frac{3 \pi a^{4}}{16}\)
Hint:

![]()
Question 20.
![]()

Solution:
(a) \(\frac{1}{2}\)
Hint:

Samacheer Kalvi 12th Maths Solutions Chapter 9 Applications of Integration Ex 9.10 Additional Problems
Choose the correct or the most suitable answer from the given four alternatives:
Question 1.
The area bounded by the line y = x, the x – axis, the ordinates x = 1,x = 2 is …….

Solution:
(a) \(\frac{3}{2}\)
Hint:
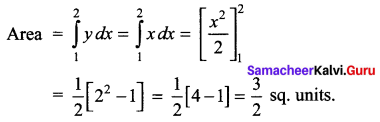
Question 2.
The area of the region bounded by the graph of y = sin x and y = cos x between x = 0 and x = \(\frac{\pi}{4}\) is ……..
![]()
Solution:
(b) \(\sqrt{2}-1\)
Hint:
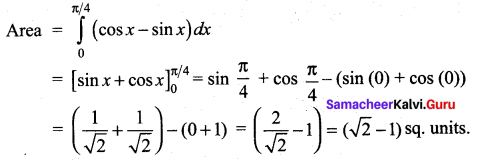
Question 3.
The area between the ellipse \(\frac{x^{2}}{a^{2}}+\frac{y^{2}}{b^{2}}\) = 1 and its auxiliary circle is …….
(a) πb(a – b)
(b) 2πa(a – b)
(c) πa(a – b)
(d) 2πb(a – b)
Solution:
(c) πa(a – b)
Hint:
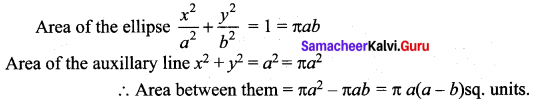
![]()
Question 4.
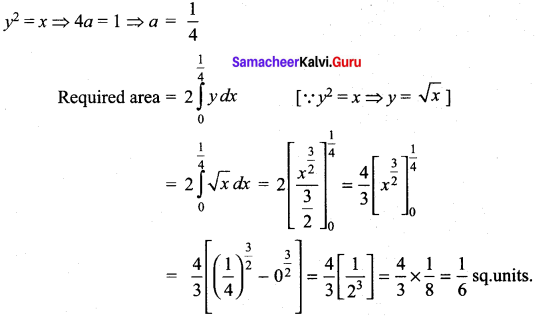
The area bounded by the parabola y2 = x and its latus rectum is ……..

Solution:
(b) \(\frac{1}{6}\)
Hint:
Question 5.
The volume of the solid obtained by revolving \(\frac{x^{2}}{9}+\frac{y^{2}}{16}\) = 1 about the minor axis is …….
(a) 48π
(b) 64π
(c) 32π
(d) 128π
Solution:
(b) 64π
Hint:
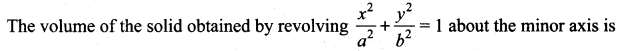
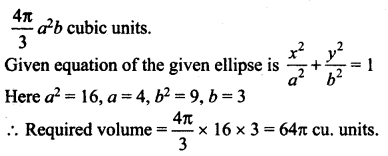
Question 6.
The volume, when the curve y = \(\sqrt{3+x^{2}}\) from x = 0 to x = 4 is rotated about x – axis is ……

Solution:
(c) \(\frac{100}{3} \pi\)
Hint:
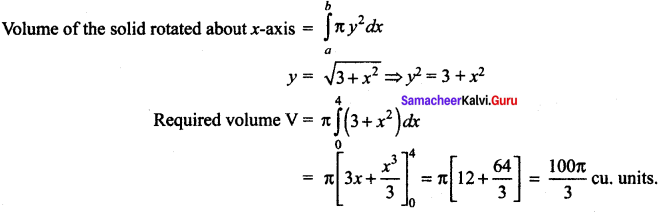
![]()
Question 7.
The volume generated when the region bounded by y = x, y = 1, x = 0 is rotated about y – axis is ……….
![]()
Solution:
(c) \(\frac{\pi}{3}\)
Hint:
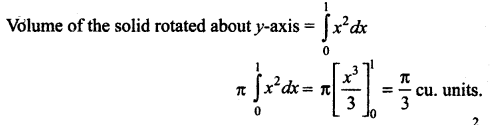
Question 8.
Volume of solid obtained by revolving the area of the ellipse \(\frac{x^{2}}{a^{2}}+\frac{y^{2}}{b^{2}}\) = 1 about major and minor axes are in the ratio …….
(a) b2 : a2
(b) a2 : b2
(c) a : b
(d) b : a
Solution:
(d) b : a
Hint:

Question 9.
The volume generated by rotating the triangle with vertices at (0, 0), (3, 0) and (3, 3) about x-axis is …….
(a) 18π
(b) 2π
(c) 36π
(d) 9π
Solution:
(d) 9π
Hint:
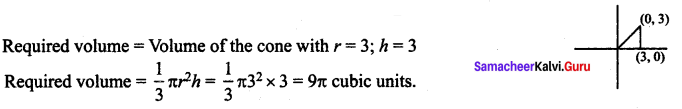
Question 10.
The length of the arc of the curve ![]() is …….
is …….
(a) 48
(b) 24
(c) 12
(d) 96
Solution:
(a) 48
Hint:
Length of the arc of the curve = 6a
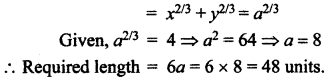
∴ Required length = 6a = 6 × 8 = 48 units.
![]()
Question 11.
The surface area of the solid of revolution of the region bounded by y = 2x, x = 0 and x = 2 about x-axis is ……
![]()
Solution:
(a) \(8 \sqrt{5} \pi\)
Hint:

Question 12.
The curved surface area of a sphere of radius 5, intercepted between two parallel planes of distance 2 and 4 from the centre is ……
(a) 20π
(b) 40π
(c) 10π
(d) 30π
Solution:
(a) 20π
Hint:
The curved surface area of a sphere of radius r intercepted between two parallel planes at a distance a and b from the centre of the sphere is 2πr (b – a)
Given radius, r = 5; a = 2; b = 4
Required surface area = 2πr (b – a)
= 2π × 5 × (4 – 2) = 20π sq. units