You can Download Samacheer Kalvi 12th Maths Book Solutions Guide Pdf, Tamilnadu State Board help you to revise the complete Syllabus and score more marks in your examinations.
Tamilnadu Samacheer Kalvi 12th Maths Solutions Chapter 5 Two Dimensional Analytical Geometry – II Ex 5.4
Question 1.
Find the equations of the two tangents that can be drawn from (5, 2) to the ellipse 2x2 + 7y2 = 14 .
Solution:
2x2 + 7y2 = 14
(÷ by 14) ⇒ \(\frac{x^{2}}{7}+\frac{y^{2}}{2}\) = 1
comparing this equation with \(\frac{x^{2}}{a^{2}}+\frac{y^{2}}{b^{2}}\) = 1
we get a2 = 7 and b2 = 2
The equation of tangent to the above ellipse will be of the form
y = mx + \(\sqrt{a^{2} m^{2}+b^{2}}\) ⇒ y = mx + \(\sqrt{7 m^{2}+2}\)
Here the tangents are drawn from the point (5, 2)
⇒ 2 = 5m + \(\sqrt{7 m^{2}+2}\) ⇒ 2 – 5m = \(\sqrt{7 m^{2}+2}\)
Squaring on both sides we get
(2 – 5m)2 = 7m2 + 2
25m2 + 4 – 20m – 7m2 – 2 = 0
18m2 – 20m + 2 = 0
(÷ by 2) ⇒ 9m2 – 10m + 1 = 0
(9m – 1) (m – 1) = 0
‘ m = 1 (or) m = 1/9
When m = 1, the equation of tangent is
y = x + 3 or x – y + 3 = 0
When m = \(\frac{1}{9}\) the equation of tangent is 9
y = \(=\frac{x}{9}+\sqrt{\frac{7}{81}+2}\) (i.e.) y = \(\frac{x}{9}+\frac{13}{9}\)
9y = x + 13 or x – 9y + 13 = 0
Question 2.
Find the equations of tangents to the hyperbola \(\frac{x^{2}}{16}-\frac{y^{2}}{64}\) = 1 which are parallel to 10x – 3y + 9 = 0.
Solution:
\(\frac{x^{2}}{16}-\frac{y^{2}}{64}\) = 1
Here a2 = 16 and b2 = 64
The equation of tangents will be of the form y = mx ± \(\sqrt{a^{2} m^{2}-b^{2}}\)
(i.e.,) y = mx ± \(\sqrt{16 m^{2}-64}\)
Where ‘m’ is the slope of the tangent.
Here we are given that the tangents are parallel to 10x – 3y + 9 = 0
So slope of tangents will be equatl to slope of the given line

![]()
Question 3.
Show that the line x – y + 4 = 0 is a tangent to the ellipse x2 + 3y2 = 12. Also find the coordinates of the point of contact.
Solution:
The given ellipse is x2 + 3y2 = 12
(÷ by 12) ⇒ \(\frac{x^{2}}{12}+\frac{y^{2}}{4}\) = 1
(ie.,) Here a2 = 12 and b2 = 4
The given line is x – y + 4 = 0
(ie.,) y = x + 4
Comparing this line with y = mx + c
We get m = 1 and c = 4
The condition for the line y = mx + c
To be a tangent to the ellipse \(\frac{x^{2}}{a^{2}}+\frac{y^{2}}{b^{2}}\) = 1 is c2 = a2m2 + b2
LHS = c2 = 42 = 16
RHS: a2m2 + b2 = 12( 1 )2 + 4 = 16
LHS = RHS The given line is a tangent to the ellipse. Also the point of contact is
\(\left(\frac{-a^{2} m}{c}, \frac{b^{2}}{c}\right)=\left[-\left(\frac{12(1)}{4}\right), \frac{4}{4}\right]\) (i.e.,) (-3, 1)
Question 4.
Find the equation of the tangent to the parabola y2 = 16x perpendicular to 2x + 2y + 3 =0
Solution:
y2 =16x
Comparing this equation with y2 = 4ax
we get 4a = 16 ⇒ a = 4
The equation of tangent to the parabola y2 = 16x will be of the form

So m = 1
⇒ The equation of tangent will be y = 1(x) + \(\frac{4}{1}\) (i.e.,) y = x + 4
(or) x – y + 4 = 0
Question 5.
Find the equation of the tangent at t = 2 to the parabola y2 = 8x. (Hint: use parametric form)
Solution:
y2 = 8x .
Comparing this equation with y2 = 4ax
we get 4a = 8 ⇒ a = 2
Now, the parametric form for y2 = 4ax is x = at2, y = 2at
Here a = 2 and t = 2
⇒ x = 2(2)2 = 8 and y = 2(2) (2) = 8
So the point is (8, 8)
Now eqution of tangent to y2 = 4 ax at (x1, y1) is yy1 = 2a(x + x1)
Here (x1, y1) = (8, 8) and a = 2
So equation of tangent is y(8) = 2(2) (x + 8)
(ie.,) 8y = 4 (x + 8)
(÷ by 4) ⇒ 2y = x + 8 ⇒ x – 2y + 8 = 0
Aliter
The equation of tangent to the parabola y2 = 4ax at ‘t’ is
yt = x + at2
Here t = 2 and a = 2
So equation of tangent is
(i.e.,) y(2) = x + 2(2)2
2y = x + 8 ⇒ x – 2y + 8 = 0
Question 6.
Find the equations of the tangent and normal to hyperbola 12x2 – 9y2 = 108 at θ = \(\frac{\pi}{3}\) .
(Hint: Use parametric form)
Solution:
12x2 – 9y2 = 108

Normal is a line perpendicular to tangent
So equation of normal will be of the form 3x + 4y + k = 0
The normal is drawn at (6, 6)
⇒ 18 + 24 + k = 0 ⇒ k = – 42
So equation of normal is 3x + 4y – 42 = 0

![]()
Question 7.
Prove that the point of intersection of the tangents at ‘t1‘ and t2’ on the parabola y2 = 4ax is [at1 t2, a (t1 + t2)].
Solution:
The equation of tangent to y2 = 4ax at ‘t’ is given by yt = x + at2
So equation of tangent at ‘t1‘ is yt1 = x + at12
and equation of tangent at ‘t2‘ is yt2 = x + at22
To find the point of intersection we have to solve the two equations

Question 8.
If the normal at the point ‘t1‘ on the parabola y2 = 4ax meets the parabola again at the point ‘t2‘, then prove that t2 = \(-\left(t_{1}+\frac{2}{t_{1}}\right)\)
Solution:
Equation of normal to y2 =4 at’ t’ is y + xt = 2at + at3.
So equation of normal at ‘t1’ is y + xt1 = 2at1 + at13
The normal meets the parabola y2 = 4ax at ‘t2’ (ie.,) at (at22, 2at2)
⇒ 2at2 + at1t22 = 2at1 + at13
So 2a(t2 – t1) = at13 – at1t22
⇒ 2a(t2 – t1) = at1(t12 – t22)
⇒ 2(t2 – t1) = t1(t1 + t2)(t1 – t2)
⇒ 2= -t1(t1 + t2)
⇒ t1 + t2 = \(\frac{-2}{t_{1}}\)
⇒ t2 = \(-t_{1}-\frac{2}{t_{1}}=-\left(t_{1}+\frac{2}{t_{1}}\right)\)
Samacheer Kalvi 12th Maths Solutions Chapter 5 Two Dimensional Analytical Geometry – II Ex 5.4 Additional Questions
Question 1.
Find the equations of the tangent and normal to the parabolas : x2 + 2x – 4y + 4 = 0 at (0, 1)
Solution:

Question 2.
Find the equations of the tangent and normal to the parabola y2 = 8x at t = \(\frac{1}{2}\)
Solution:

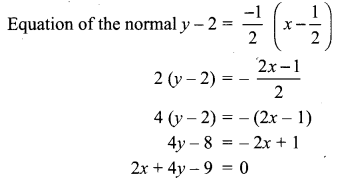
∴ Equation of the tangent is 2x – y + 1 = 0 and equation of the normal is 2x + 4y – 9 = 0
Question 3.
Find the equations of the tangents: to the parabola y2 = 6x, parallel to 3x – 2y + 5 = 0
Solution:

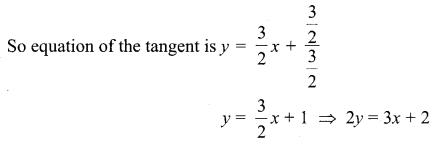
∴ Equation of the tangent is 3x – 2y + 2 = 0
Question 4.
Find the equations of the tangents: to the parabola 4x2 – y2 = 64 Which are parallel to 10x – 3y + 9 = 0.
Solution:

Question 5.
Find the equation of the tangent from point (2, -3) to the parabola y2 = 4x.
Solution:
y2 = 4x
Equation of the tangent to the parabola will be of the form y = \(m x+\frac{1}{m}\)
The tangents pass through (2, -3)
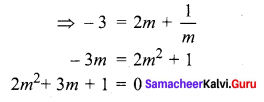
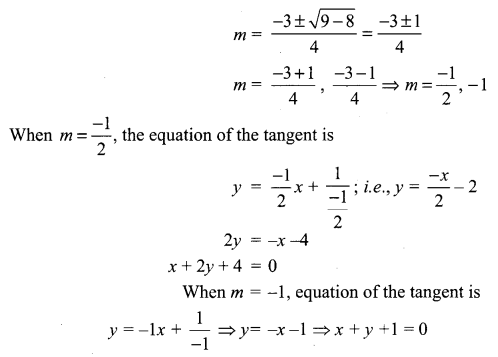
The two tangents drawn from (2, -3) are x + y + 1 = 0, x + 2y + 4 = 0
![]()
Question 6.
Find the equation of the tangents from the point (2, -3) to the parabola 2x2 – 3y2 = 6
Solution:
2x2 – 3y2 = 6

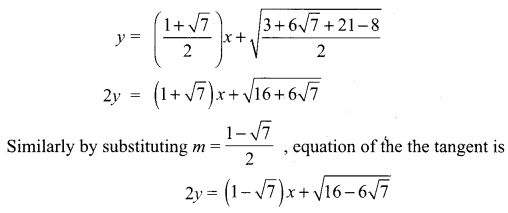
Question 7.
Prove that the line 5x + 12y = 9 touches the hyperbola x2 – 9y2 = 9 and find the point of contact.
Solution:
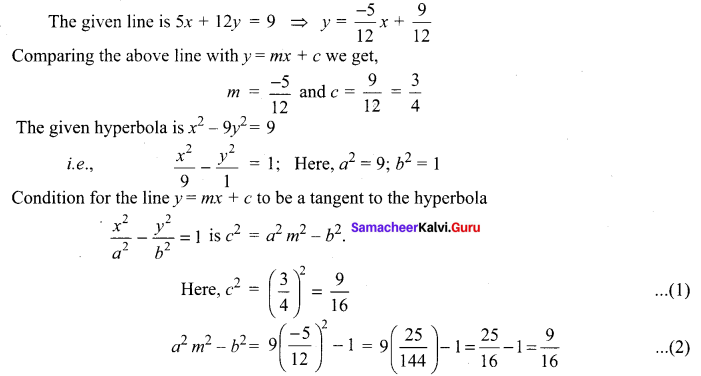
(1) = (2) ⇒ The given line is a tangent to the curve i.e., the given line touches the curve. To find the point of contact we have to solve the line and the curve.
The given line 5x + 12y = 9

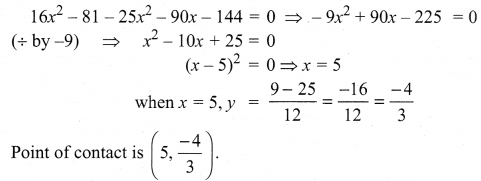
Question 8.
Show that the line x – y + 4 = 0 is a tangent to the ellipse x2 + 3y2 = 12. Find the co-ordinates of the point of contact.
Solution:
The given ellipse is x2 + 3y2 = 12
Given line is x – y + 4 = 0 ⇒ y = x + 4
Here, m = 1 and c = 4
The condition for the line y = mx + c to be a tangent to the ellipse
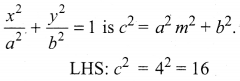
RHS: a2 m2 + b = 12(1) + 4 = 16
LHS: RHS ⇒ the given lines is a tangent to the ellipse.