Samacheer Kalvi 12th Maths Solutions Chapter 1 Applications of Matrices and Determinants Ex 1.2

You can Download Samacheer Kalvi 12th Maths Book Solutions Guide Pdf, Tamilnadu State Board help you to revise the complete Syllabus and score more marks in your examinations.

Tamilnadu Samacheer Kalvi 12th Maths Solutions Chapter 1 Applications of Matrices and Determinants Ex 1.2

Question 1.
Find the rank of the following matrices by the minor method:


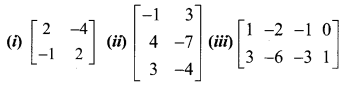
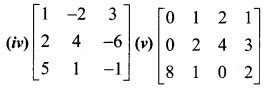
Solution:

Question 2.
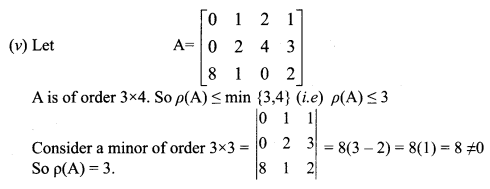
Find the rank of the folowing matrices by row reduction method:

Solution:
(i) Let

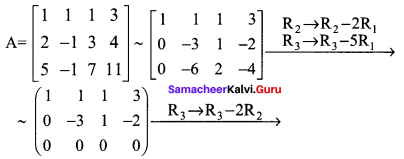
The last equivalent matrix is in row-echelon form. It has three non zero rows. So ρ(A) = 3
(ii) Let

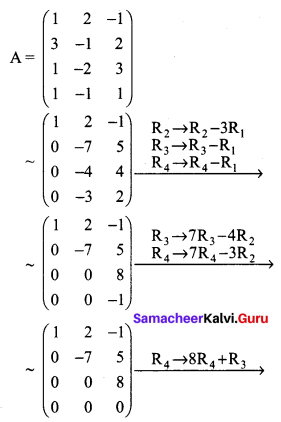
The last equivalent matrix is in row-echelon form. It has three non zero rows. ρ(A) = 3
(iii) Let

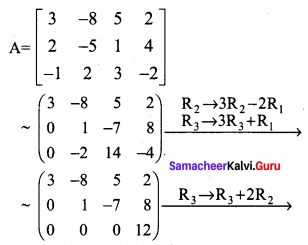
The last equivalent matrix is in row-echelon form. It has three non zero rows. ρ(A) = 3

Question 3.
Find the inverse of each of the following by Gauss-Jordan method:

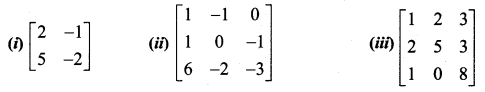
Solution:
(i) Let \(A=\left(\begin{array}{cc}{2} & {-1} \\ {5} & {-2}\end{array}\right)\)
Applying Gauss-Jordan method we get

(ii) Let


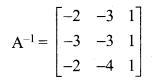
(iii) Let

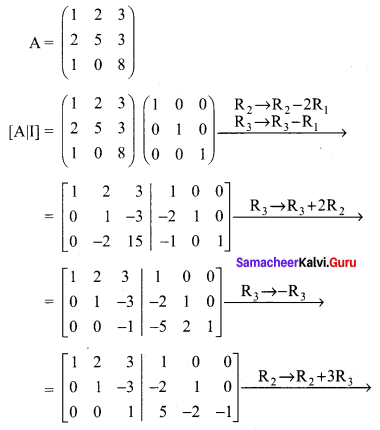
Samacheer Kalvi 12th Maths Solutions Chapter 1 Applications of Matrices and Determinants Ex 1.2 Additional Problems

Question 1.
Find the rank of the following matrices.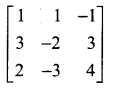
Solution:

A has at least one non-zero minor of order 2. \(\rho(\mathrm{A})\) = 2

Question 2.
Find the rank of the following matrices.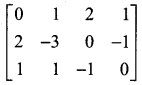
Solution:

The last equivalent matrix is in the echelon form. It has three non-zero rows.
∴ \(\rho(\mathrm{A})\) = 3; Here A is of order 3 × 4

Question 3.
Find the rank of the following matrices.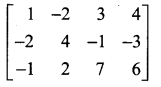
Solution:


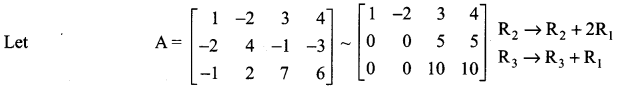
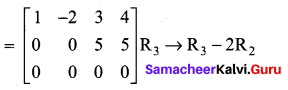
The last equivalent matrix is in the echelon form. The number of non-zero rows in this matrix is two. A is a matrix of order 3 × 4. ∴ \(\rho(\mathrm{A})\) = 2

Question 4.
Using elementary transformations find the inverse of the following matrix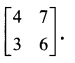
Solution:

Question 5.
Using elementary transformations find the inverse of the following matrices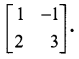
Solution:

Question 6.
Using elementary transformations find the inverse of the following matrices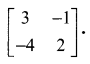
Solution:

Question 7.
Using elementary transformations, find the inverse of the following matrices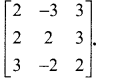
Solution:

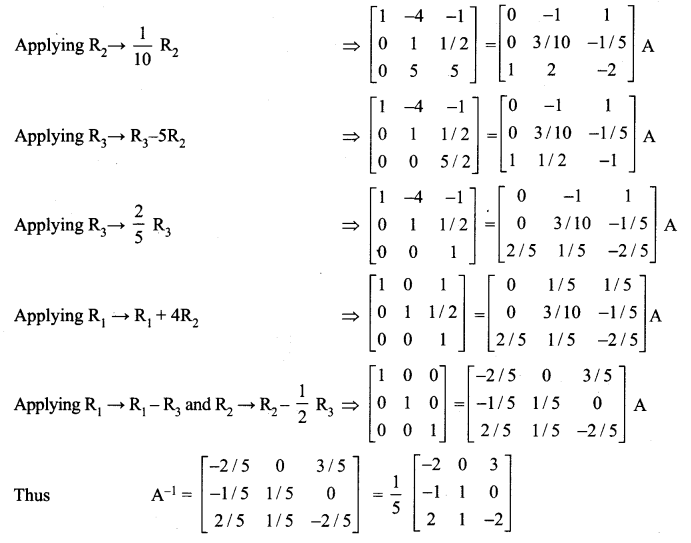
Question 8.
Using elementary transformations, find the inverse of the following matrices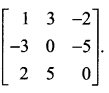
Solution:

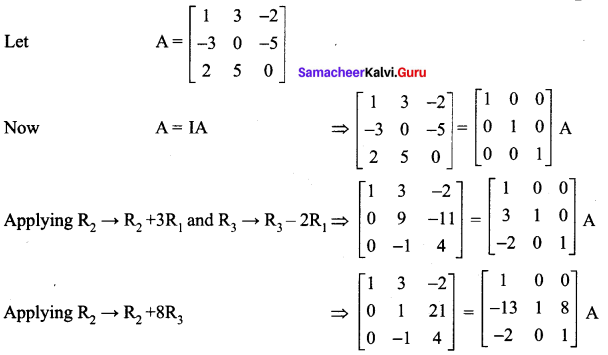
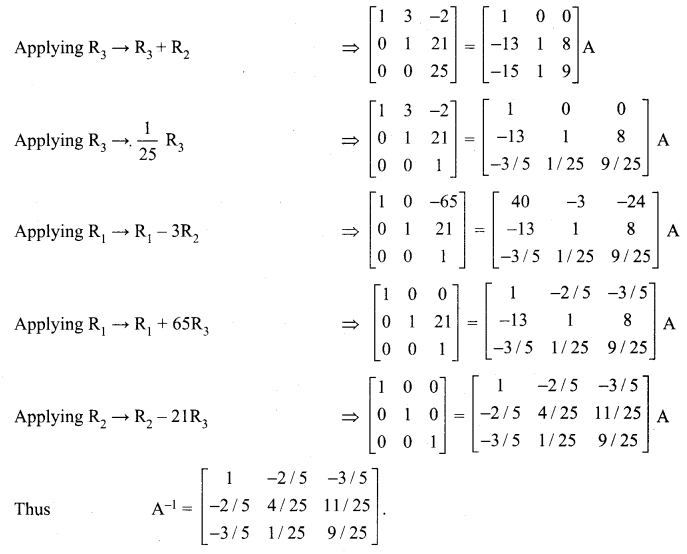
Question 9.
Using elementary transformations, find the inverse of the following matrices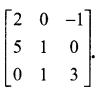
Solution:

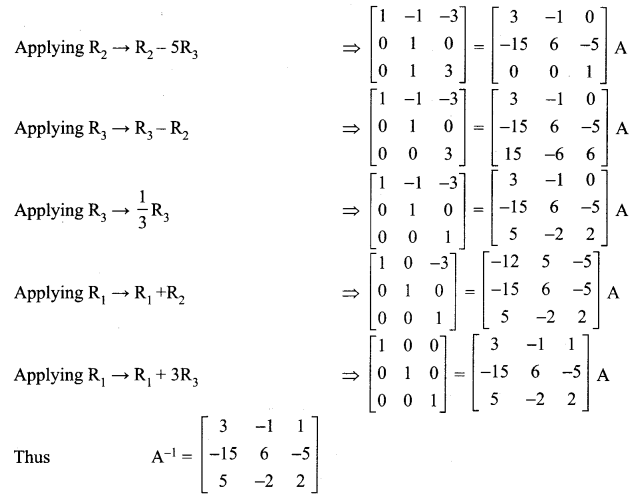
Question 10.
Using elementary transformations, find the inverse of the following matrices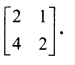
Solution:

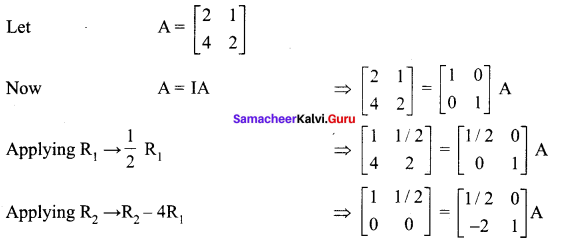
Since R₂ has all numbers zero, Thus inverse of matrix A does not exist.