Samacheer Kalvi 12th Maths Guide Chapter 3 சமன்பாட்டியல் Ex 3.6

Tamilnadu State Board New Syllabus Samacheer Kalvi 12th Maths Guide Pdf Chapter 3 சமன்பாட்டியல் Ex 3.6 Textbook Questions and Answers, Notes.

TN Board 12th Maths Solutions Chapter 3 சமன்பாட்டியல் Ex 3.6

கேள்வி 1.
9x⁹ – 4x⁸ + 4x⁷ – 3x⁶ + 2x⁵ + x³ + 7x² + 7x + 2 = 0 எனும் பல்லுறுப்புக்கோவை சமன்பாட்டின் அதிகபட்ச சாத்தியமான மிகை எண் மற்றும் குறையெண் மூலங்களின் எண்ணிக்கையை ஆராய்க.
தீர்வு:
p(x) = 9x⁹ – 4x⁸ + 4x⁷ – 3x⁶ + 2x⁵
+ x³ + 7x² + 7x + 2 = 0 என்க
p(x) ன் குறிகளை பின்வருமாறு எழுதலாம்:

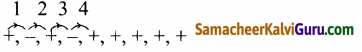
p(x) க்கு 4 முறை குறி மாற்றம் நிகழ்ந்துள்ளது மற்றும் p(x)-ன் மிகை பூச்சியமாக்கிகளின் எண்ணிக்கை 4 – க்கு மிகாது.
மேலும் p(-x) = 9(-x)⁹ – 5(-x)⁸ – 4(-x)⁷ – 3(-x)⁶ + 2(-x)⁵ + (-x)³ + 7 (-x)² + 7(-x) + 2
p(-x) =-9x⁹ – 4x⁸ – 4x⁷ – 3x⁶ – 2x⁵ – x³ + 7x² – 7x + 2
p(-x) – ன் குறிகள்

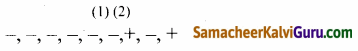
p(-x)
எனவே p(-x)க்கு இரண்டு முறை குறி மாற்றம் நிகழ்ந்துள்ளது.
p(x)க்கு அதிகபட்சம் இரண்டு குறை.

கேள்வி 2.
x² – 5x + 6 மற்றும் x² – 5x + 16 ஆகிய பல்லுறுப்புக் கோவைகளின் அதிகபட்ச சாத்தியமான மிகை எண் மற்றும் குறையெண் பூச்சியமாக்கிகளின் எண்ணிக்கையை ஆராய்க. வளைவரைகளின் தோராய வரைபடம் வரைக.
தீர்வு:
p(x) = x² – 5x + 6 என்க
p(x) க்கு இரண்டு குறி மாற்றங்கள் நிகழ்ந்துள்ளது. ஆகையால் p(x) க்கு அதிகபட்சம் இரண்டு மெய் மூலங்கள் இருக்கும்.
Q(x) = x² – 5x + 16 என்க.
p(- x) = (-x)² – 5 (-x) + 6
= x² + 5x + 6
p(- x)க்கு குறி மாற்றம் இல்லை. எனவே குறை மூலங்கள் இல்லை.
Q(x) = x² – 5x + 6 என்க.
Q(x)க்கு இரண்டு குறி மாற்றம் நிகழ்ந்துள்ளது மற்றும் Q(-x)க்கு குறி மாற்றம் இல்லை.
[∵ Q(-x) = (-x)² -5(-x) + 16 = x² + 5x + 16]
∴ அதற்கு அதிகபட்சம் இரண்டு மிகை மூலங்கள் மற்றும் குறை மூலங்கள் இல்லை.

கேள்வி 3.
x⁹ – 5x⁵+ 4 + 2x² + 1 = 0 என்ற சமன்பாட்டிற்கு குறைந்தபட்சம் 6 மெய்யற்ற கலப்பெண்
தீர்வுகள் உண்டு எனக் காட்டுக.
தீர்வு:
p(x) x⁹ – 5x⁵ + 4x⁴ + 2x² + 1 = 0 என்க
குறிகள் +, -, +, +, +
p(x)-ல் இரண்டு குறிமாற்றம் நிகழ்ந்துள்ளது.
மேலும் p(-x) = (-x)⁹ -5(-x)⁵ + 4(-x)⁴ + 2(-x)⁹ + 1 = 0
p(-x) =-x⁹ + 5x⁵ + 4x⁴ + 2x² + 1 = 0
p(-x)க்கு ஒரே ஒரு குறி மாற்றம்.
∴ p(x) க்கு அதிகபட்சம் இரண்டு மிகை மூலம் மற்றும் 1 குறை மூலம் உள்ளது.
p(x) – ன் படி 9, ஆதலால் p(x)க்கு குறைந்தபட்சம் 6 கற்பனை தீர்வுகள் உள்ளன.

கேள்வி 4.
x⁹ – 5x³ – 14x⁷ = 0 எனும் பல்லுறுப்புக்கோவை சமன்பாட்டின் மிகையெண் மற்றும் குறையெண் மூலங்களின் எண்ணிக்கையை தீர்மானிக்க.
தீர்வு:
p(x) = x⁹ – 5x² – 14x⁷ = 0 என்க
p(x) க்கு ஒரே ஒரு குறி மாற்றம் நிகழ்ந்துள்ளது.
மேலும் p(-x) = (-x)⁹ – 5(-x)⁸ – 14(-x)⁷ = 0
⇒ p(-x) = – x⁹ – 5x⁸ + 14x⁷ = 0
p(-x) க்கு ஒரே ஒரு குறி மாற்றம் நிகழந்துள்ளது.
∴ p(-x) -க்கு அதிகபட்சம் ஒரு மிகை மற்றும் ஒரு குறை மூலம் உள்ளது.

கேள்வி 5.
x⁹ + 9x⁷ + 7x⁵ + 5x³ + 3x எனும் பல்லுறுப்புக்கோவையின் மெய்யெண் மற்றும் மெய்யற்ற கலப்பெண் பூச்சியமாக்கிகளின் துல்லியமான எண்ணிக்கையைக் கண்டறிக.
தீர்வு:
p(x) = x⁹ + 9x⁷ + 7x⁵ + 5x³ + 3x என்க
p(x) க்கு குறி மாற்றம் இல்லை.
p(-x) = (-x)⁹ + 9(-x)⁷ + 7(-x)⁵ + 5(-x)³ + 3(-x)
= – x⁹ – 9x⁷ – 7x⁵ – 5x³ – 3x
p(-x) க்கு குறி மாற்றம் இல்லை
∴ p(x) க்கு மிகை மற்றும் குறை மூலங்கள் இல்லை.