Samacheer Kalvi 12th Maths Guide Chapter 3 சமன்பாட்டியல் Ex 3.1

Tamilnadu State Board New Syllabus Samacheer Kalvi 12th Maths Guide Pdf Chapter 3 சமன்பாட்டியல் Ex 3.1 Textbook Questions and Answers, Notes.

TN Board 12th Maths Solutions Chapter 3 சமன்பாட்டியல் Ex 3.1

கேள்வி 1.
ஒரு கனச் சதுரப் பெட்டியின் பக்கங்களை 1, 2, 3 அலகுகள் அதிகரிப்பதால் கனச்சதுரப் பெட்டியின் கொள்ளவைவிட 52 கன அலகுகள் அதிகமுள்ள கனச் செவ்வகம் கிடைக்கிறது. எனில், கன செவ்கத்தின் கொள்ளவைக் காண்க.
தீர்வு:
கனச் செவ்வகத்தின் நீளம் மற்றும் அகலம் x + 1, x + 2, மற்றும் x + 3
[∵ 1, 2, 3 அலகுகள் அதிகரிப்பதால்]
மேலும் கொள்ளளவு = V + 52
[V என்பது அதிகரிப்பதால் 52]
∴ V + 52 = (x + 1) (x + 2) (x + 3) —- (1)
⇒ V = (x + 1) (x + 2) (x + 3) – 52
இங்கு α = -1, β = -2, γ = -3
⇒ V = x³ – x² (α + β + γ) + x (αβ + βγ + γα) – αβγ – 52
⇒ v = x³ – x²(-1 – 2 – 3) + x (2 + 6 + 3) – (-1) (-2)(-3) – 52
⇒ V = x³ – x²(-6) + x(11) + 6 – 52.
⇒ x³ = x³ + 6x² + 11x + 6 – 52

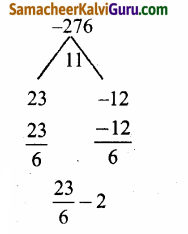
⇒ 06x² + 11x – 46 = 0
⇒ (6x + 23)(x – 2) = 0
⇒ (6x + 23) (x – 2) = 0
⇒ x = 2
∵ கனச்சதுரத்தின் கொள்ளளவு = x³ = 2³ = 8 கன அலகுகள்
[∵ x = \(\frac{-23}{6}\) என்பது சாத்தியமில்லை x ஆனது கனத்தின் பக்கத்தை குறிக்கிறது]

கேள்வி 2.
கொடுக்கப்பட்ட மூலங்களைக் கொண்டு முப்படி சமன்பாடுகளை உருவாக்குக.
(i) 1,2, மற்றும் 3
(ii) 1,1, மற்றும் – 2
(iii) 2, \(\frac{1}{2}\) மற்றும் 1
தீர்வு:
கொடுக்கப்பட்ட மூலங்கள் 1,2 மற்றும் 3
இங்கு α = 1, β = 2 மற்றும் γ= 3
α, β, γ என்பது மூலங்களாக உடைய ஒரு முப்படி சமன்பாடு
x³ – (α + β + γ)x² + (αβ + βγ + γα)x – αβγ = 0
⇒ x³ – (1 + 2 + 3) x² + (2 + 6 + 3)x – 6 = 0
⇒ x³ – 6x² + 11x – 6 = 0.

(ii) இங்கு α = 1, β = 1 மற்றும் γ = -2
∴ தேவையான முப்படி சமன்பாடு
x³ – (1 + 1 – 2)x² + (1 – 2 – 2)x – (1)(1)(-2) = 0
x³ – 0x² – 3x + 2 = 0
x³ – 3x + 2 = 0.

(iii) இங்கு α = 2, β = -2 மற்றும் γ = 4
∴ முப்படி சமன்பாடு
x³ – (2 – 2 + 4)x² + (-4 – 8 + 8)x – (2)(-2)(4) = 0
⇒ x³ – 4x² – 4x + 16 = 0

கேள்வி 3.
x³ + 2x² + 3x + 4 = 0, எனும் முப்படி சமன்பாட்டின் மூலங்கள் α, β மற்றும் γ எனில் கீழ்க்காணும் மூலங்களைக் கொண்டு முப்படி சமன்பாடுகளை உருவாக்குக.
(i) 2α, 2β மற்றும் 2γ,
(ii) \(\frac{1}{\alpha}\), \(\frac{1}{\βeta}\) மற்றும் \(\frac{1}{\gamma}\)
(iii) -α, -β மற்றும் -γ
தீர்வு:
x³ + 2x² + 3x + 4 = 0 மூலங்கள் α, β, γ
∴ α + β + γ = – x² – ன் கெழு = -2 …. (1)
αβ + βγ + γα = x -ன் கெழு = 3 … (2)
-αβγ = +4 ⇒ αβγ = -4 …..(3)
(i) 2α, 2β, 2γ வை மூலங்களாக உடைய முப்படி சமன்பாட்டை உருவாக்க
2α + 2β + 2γ = 2 (α + β + γ) = 2 (- 2) = -4 [(1) லிருந்து]
4αβ + 4βγ + 4γα = 4 (αβ + βγ + γα) = 4(3) = 12 [(2) லிருந்து]
(2α) (2β) (2γ) = 8(αβγ) = 8( 4) = -32 [(3) லிருந்து]
∴ தேவையான முப்படி சமன்பாடு
x³ – (2α + 2β + 2γ) x² + (2αβ + 2βγ + 2γα) x – (2α) (2β) (2γ) = 0
⇒ x³ – (-4)x² + 12x + 32 = 0
⇒ x +4x² + 12x + 32 = 0

(ii) \(\frac{1}{\alpha}\), \(\frac{1}{\beta}\), \(\frac{1}{\gamma}\) வை மூலங்களாக உடைய முப்படி சமன்பாட்டை உருவாக்க


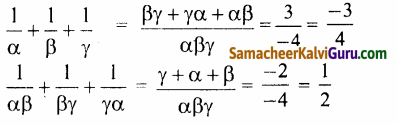
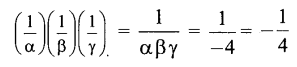
∴ தேவையான முப்படி சமன்பாடு

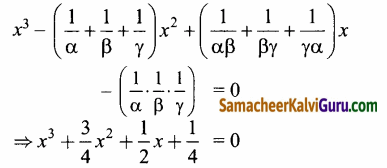
4 ஆல் பெருக்கக் கிடைப்பது
4x³ + 3x² + 2x + 1 = 0

(iii) – α – β – γ γவை மூலங்களாக உடைய சமன்பாடு
∴ -α – β – γ = – (α + β + γ)
= -(-2) = 2
αβ + βγ + γα = 3
(- α) (- β) (- γ) = – (αβγ) =-(-4) = 4
∴ தேவையான முப்படி சமன்பாடு
x³ – (-α – β – γ) x² + (αβ + βγ + γα)
x- [(-α) (- β) (-γ)] = 0
⇒ x³ – (2)x² + 3x – 4 = 0
⇒ x³ – 2x² + 3x – 4 = 0

கேள்வி 4.
3x³ – 16x² + 23x – 6 = 0 எனும் சமன்பாட்டின் இரு மூலங்களின் பெருக்கல் 1 எனில் சமன்பாட்டினைத் தீர்க்க.
தீர்வு:
கொடுக்கப்பட்ட முப்படி சமன்பாடு
3x³ – 16x² + 23x – 6 = 0
α, \(\frac{1}{\alpha}\) மற்றும் γ என்பது சமன்பாட்டின் மூலங்கள்
[ ∵ இரண்டு மூலங்களின் பெருக்கல் பலன் 1]
(1) → x³ – \(\frac{16}{3}\)x² + \(\frac{23}{3}\) – 2 =0 ….(1)
(1) ஒப்பிடும் போது

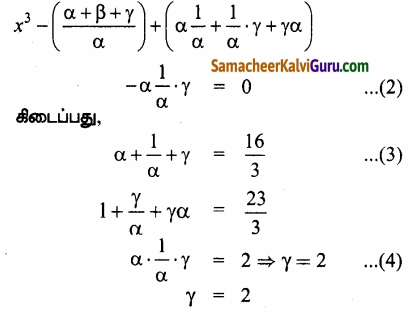
என (3)-ல் பிரதியிட கிடைப்பது
α + \(\frac{1}{\alpha}\) + 2 = \(\frac{16}{3}\)
⇒ α + \(\frac{1}{\alpha}\) = \(\frac{16}{3}\) – 2 = \(\frac{16-16}{3}\) = \(\frac{10}{3}\)
⇒ \(\frac{\alpha^{2}+1}{\alpha}\) = \(\frac{10}{3}\)
3x² + 3 = 10α
3α² – 10α + 3 = 0

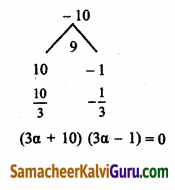
α = \(\frac{-10}{3}\)
அல்லது α = \(\frac{1}{3}\)
(3α + 10) (3α – 1) = 0
α = \(\frac{-10}{3}\) சாத்தியமில்லை
⇒ α = \(\frac{1}{3}\)
[∵ α = \(\frac{-10}{3}\) (5)ஐ நிறைவு செய்யவில்லை]
∴ மூலங்கள் 3, \(\frac{1}{3}\), 2.

கேள்வி 5.
2x⁴ – 8x³ + 6x² – 3 = 0 எனும் சமன்பாட்டின் மூலங்களின் வர்க்கங்களின் கூடுதல் காண்க.
தீர்வு:
கொடுக்கப்பட்ட சமன்பாடு 2x⁴ – 8x³ + 6x² – 3 = 0
இங்கு a = 2, b = -8, c = 6, d = 0, e =-3
α, β, γ மற்றும் δ என்பது சமன்பாடு (1)-ன் மூலங்கள் என்க.
வியட்டாவின் சூத்திரப்படி,

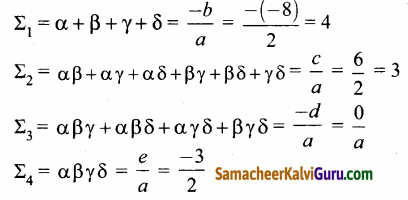
இப்பொழுது (a + b + c + d) = a² + b² + c² + d² + 2 (ab + ac + ad + bc + cd)
⇒ α² + β² +γ² + δ² = (a + β + γ + δ)²
– 2(αβ + αγ + αδ+ βγ + βδ + γδ)
α² + β² + γ² + δ² = 4² – 2(3) = 16 – 6 = 10

கேள்வி 6.
x³ – 9x + 14x + 24 = 0 எனும் சமன்பாட்டின் இரு மூலங்கள் 3 : 2 என்ற விகிதத்தில் அமைந்தால், சமன்பாட்டை தீர்க்க.
தீர்வு:
α, β, γ என்பது சமன்பாட்டின் மூலங்கள் என்க கொடுக்கப்பட்ட \(\frac{\alpha}{\beta}\) = \(\frac{3}{2}\) ⇒ 2α = 3β ⇒ α = \(\frac{3}{2}\)β
∴ \(\frac{3}{2}\)β, β, γ என்பது கொடுக்கப்பட்ட சமன்பாட்டின் மூலங்கள் வியட்டாவின் சூத்திரப்படி,

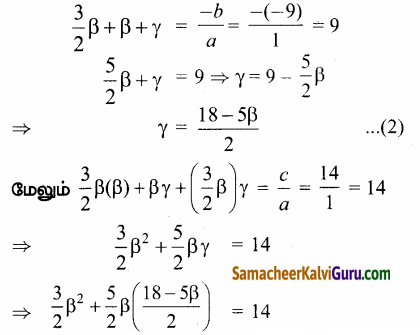
[(2)ஐ பயன்படுத்தி]

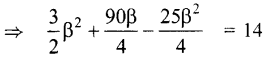
4 ஆல் பெருக்க 6β² + 90β – 25β² = 56
19β² – 90β + 56 = 0
(β – 4)(19β – 14) = 0
⇒ β = 4
β = \(\frac{14}{19}\)



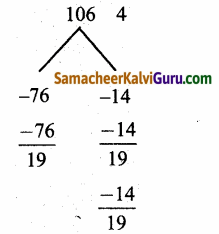
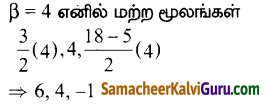
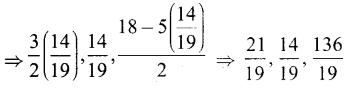
β = \(\frac{14}{9}\) எனில் மற்ற மூலங்கள் \(\frac{3}{2}\)β, β, \(\frac{18-5 \beta}{2}\)
[(2)-ன் படி]

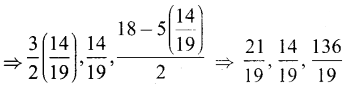
கேள்வி 7.
α, β மற்றும் γ ஆகியன ax³ + bx² + cx + d = 0 எனும் பல்லுறுப்புக்கோவை சமன்பாட்டின் மூலங்களாக இருப்பின், கெழுக்கள் வாயிலாக \(\sum \frac{a}{\beta \gamma}\) -ன் மதிப்பைக் காண்க.
தீர்வு:
கொடுக்கப்பட்ட ax³ + bx² + cx + d = 0 -ன் மூலங்கள் α, β மற்றும் γ
∴ α + β + γ = \(\frac{-b}{a}\)
αβ + βγ + γα = \(\frac{c}{a}\)
αβγ = –\(\frac{d}{a}\)

கேள்வி 8.
α, β, γ மற்றும் δ ஆகியன 2x⁴ + x³ – 7x² + 8 = 0 எனும் பல்லுறுப்புக்கோவை சமன்பாட்டின் மூலங்கள் எனில், α + β + γ + δ மற்றும் α β γ δ ஆகியவற்றினை மூலங்களாகவும் முழு எண்களை கெழுக்களாகவும் கொண்ட ஓர் இருபடி சமன்பாட்டைக் காண்க.
தீர்வு:
கொடுக்கப்பட்ட பல்லுறுப்புக் கோவை சமன்பாடு
2x⁴ + 5x³ – 7x² + 8 = 0
இங்கு a = 2, b = 5, c = -7, d = 0, e = 8
வியட்டாவின் சூத்திரப்படி,
α + β + γ + δ = –\(\frac{b}{a}\) = –\(\frac{5}{2}\)
αβ + αγ + αδ + βγ + βδ + γδ = \(\frac{c}{a}\) = –\(\frac{7}{2}\)
αβγ + αβδ + αγδ + βγδ = –\(\frac{d}{a}\) = 0
aβγδ = \(\frac{e}{a}\) = \(\frac{8}{2}\) = 4
கொடுக்கப்பட்ட இருபடி சமன்பாட்டின் மூலங்கள் α + β + γ + δ மற்றும் αβγδ
∴ மூலங்களின் கூடுதல் = (α + β + γ + δ) (αβγδ)

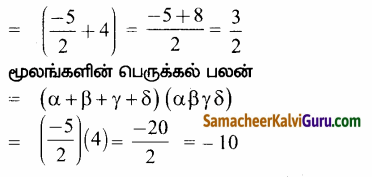
∴ தேவையான இருபடிச் சமன்பாடு x² – x (மூலங்களின் கூடுதல்) + மூலங்களின் பெருக்கல் பலன் = 0
⇒ x² – x\(\left(\frac{3}{2}\right)\) – 10 = 0
⇒ 2x² – 3x – 20 = 0

கேள்வி 9.
lx² + nx + n = 0 எனும் சமன்பாட்டின் மூலங்கள் p மற்றும் q எனில், \(\sqrt{\frac{p}{q}}\) + \(\sqrt{\frac{q}{p}}\) + \(\sqrt{\frac{n}{1}}\) = 0 எனக்
தீர்வு:
கொடுக்கப்பட்ட lx² + nx + n = 0 – ன் மூலங்கள் p, q.
இங்கு a = l, b = +n, c = n


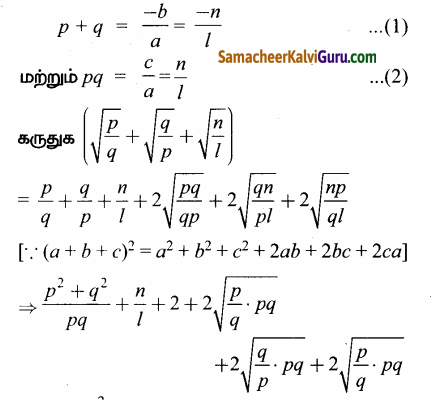
இருபுறமும் வர்க்க மூலம் காண, கிடைப்பது
\(\sqrt{\frac{p}{q}}\) + \(\sqrt{\frac{q}{p}}\) + \(\sqrt{\frac{n}{1}}\) = 0

கேள்வி 10.
x² + px +q= 0 மற்றும் x² + p’x + q’ = 0 ஆகிய இரு சமன்பாடுகளுக்கும் ஒரு பொதுவான மூலம் இருப்பின், அம்மூலம் \(\frac{p q^{\prime}-p^{\prime} q}{q-q^{\prime}}\) அல்லது \(\frac{\boldsymbol{q}-\boldsymbol{q}^{\prime}}{\boldsymbol{p}^{\prime}-\boldsymbol{p}}\) அல்லது
\(\frac{q-q^{\prime}}{p^{\prime}-p}\) ஆகும் எனக்
தீர்வு:
கொடுக்கப்பட்ட சமன்பாடு x² + px + q = 0 …. (1)
மற்றும் x² + p’x + q’ = 0 …. (2)
α என்பது (1) மற்றும் (2)-ன் பொது மூலம்
∴ α² + pα + q = 0 … (3)
மற்றும் α² + p’ α + q’ = 0 … (4)
(3) மற்றும் (4) ஐ குறுக்கு பெருக்கல் முறையில் தீர்க்க கிடைப்பது

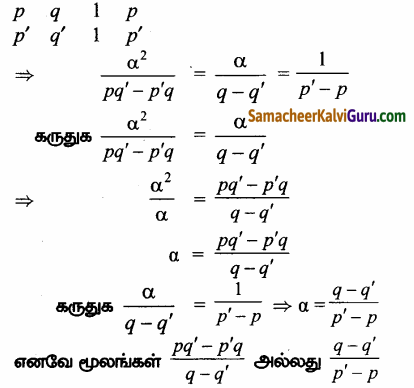
கேள்வி 11.
ஒரு எண்ணை அதன் கனமூலத்தோடு கூட்டினால் 6 கிடைக்கிறது. எனில் அந்த எண்ணைக் காணும் வழியை கணிதவியல்
கணக்காக மாற்றுக.
தீர்வு:
அந்த எண் x என்க. ∴ \(\sqrt[3]{x}\) + x = 6
⇒ \(\sqrt[3]{x}\) = 6 – x
இருபுறமும் 3 ஆம் அடுக்கை எடுக்க கிடைப்பது
\(\left(x^{\frac{1}{3}}\right)^{3}\) = (6 – x)³
x = 6³ – 3(6²)x + 3(6)(x²) – x³
[∵ (a – b)³ = a³ – 3a²b + 3ab² – b³]
⇒ x = 216 – 108x + 18x² – x³
⇒ x³ + 108x – 18x – 216 + x = 0
⇒ x³ + 18x² + 109x – 216 = 0 என்ப து
தேவையான கணிதவியல் கணக்கு.

கேள்வி 12.
12 மீட்டர் உயரமுள்ள ஒரு மரம் இரு பகுதிகளாக முறிந்துள்ளது. முறிந்த இடம் வரை இருக்கும் கீழ்ப்பகுதி, உடைப்பின் மேற்பகுதியின் நீளத்தின் கனமூலம் ஆகும். இந்தத் தகவலை கீழ்ப்பகுதியின் நீளம் காணும் வகையில் கணிதவியல் கணக்காக மாற்றுக.
தீர்வு:
கொடுக்கப்பட்ட மரத்தின் உயரம் 12 மீ.
கீழ்ப்பகுதியின் நீளம் ‘x’ மீ, உடைப்பின் மேல்பகுதியின் நீளம் (12 – x) மீ என்க.

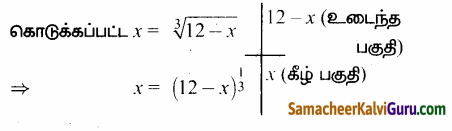
இருபுறமும் 3-ன் அடுக்கை எடுக்க கிடைப்பது,
⇒ x³ = 12 – x
⇒ x³ + x – 12 = 0 என்பது தேவையான கணிதவியல் கணக்கு.