Samacheer Kalvi 12th Maths Guide Chapter 11 நிகழ்தகவு பரவல்கள் Ex 11.2

Tamilnadu State Board New Syllabus Samacheer Kalvi 12th Maths Guide Pdf Chapter 11 நிகழ்தகவு பரவல்கள் Ex 11.2 Textbook Questions and Answers, Notes.

TN Board 12th Maths Solutions Chapter 11 நிகழ்தகவு பரவல்கள் Ex 11.2

கேள்வி 1.
மூன்று சீரான நாணயங்கள் ஒரே நேரத்தில் சுண்டப்படுகின்றன. கிடைக்கும் தலைகளின் எண்ணிக்கைக்கான நிகழ்தகவு நிறை சார்பினைக் காண்க.
தீர்வு:
கூறுவெளி S = {HHH, HHT, HTH, THH, HTT, THT, TTH, TTT}
X என்பது தலைகளின் எண்ணிக்கையை குறிக்கிறது என்க.

p(x = 0)
p(தலை இல்லை) = p(TTT)= \(\frac{1}{2}\) × \(\frac{1}{2}\) × \(\frac{1}{2}\) = \(\frac{1}{8}\)

p(x = 1) = p(1 தலை) = p(THT, HTT, TTH)
= \(\frac{1}{8}\) + \(\frac{1}{8}\) + \(\frac{1}{8}\) = \(\frac{3}{8}\)
∵ p(H) = \(\frac{1}{2}\) p(T) = \(\frac{1}{2}\)

p(x = 2) = p(2 தலைகள்) = p(HHT, HTH, THH)
= \(\frac{1}{8}\) + \(\frac{1}{8}\) + \(\frac{1}{8}\) = \(\frac{3}{8}\)

p(x = 3) = p(3 தலைகள்) = p(HHH) = \(\frac{1}{8}\)
∴ X எடுத்துக் கொள்ளும் மதிப்புகள் 0,1, 2, 3.
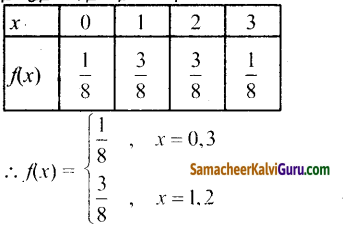
நிகழ்தகவு நிறை சார்பு
Samacheer Kalvi 12th Maths Guide Chapter 11 நிகழ்தகவு பரவல்கள் Ex 11.2 1

கேள்வி 2.
ஓர் அறுபக்க பகடையின் ஒரு பக்கத்தில் ‘1’ எனவும், இரு பக்கங்களில் ‘3’ மூன்று எனவும், மற்றும் ஏனைய மூன்று பக்கங்களில் ‘5’ எனவும் குறிக்கப்பட்டுள்ளது. பகடை இருமுறை வீசப்படுகிறது. இருமுறை வீசப்பட்டதின் மொத்த எண்ணிக்கையை X குறிக்கிறது.

(i) நிகழ்தகவு நிறை சார்பு
(ii) குவிவு பரவல் சார்பு
(iii) P(4 ≤ X < 10)
(iv) P(X ≥ 6)
தீர்வு:
பகடையின் மீதுள்ள எண்கள் 1, 3, 3, 5, 5, 5 இருமுறை வீசப்பட்டதின் மொத்த எண்ணிக்கையை X குறிக்கிறதெனில், அது எடுத்துக் கொள்ளும் மதிப்புகள் 2, 4, 6, 8, 10.
கூறுவெளி S
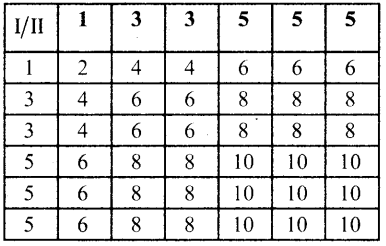
Samacheer Kalvi 12th Maths Guide Chapter 11 நிகழ்தகவு பரவல்கள் Ex 11.2 2
கூறுவெளி S -சிலிருந்து நமக்கு கிடைப்பது

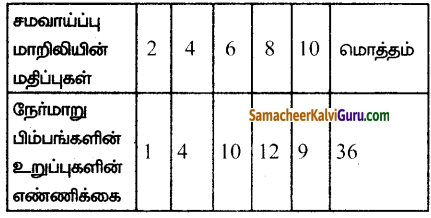
p(x = 2) = \(\frac{1}{36}\)
p(x = 4) = \(\frac{4}{36}\)
p(x = 6) = \(\frac{10}{36}\)
p (x = 8) = \(\frac{12}{36}\)
p(x = 10) = \(\frac{9}{36}\)

(i) நிகழ்தகவு நிறைச்சார்பு
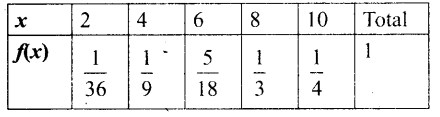
Samacheer Kalvi 12th Maths Guide Chapter 11 நிகழ்தகவு பரவல்கள் Ex 11.2 4

(ii) குவிவு பரவல் சார்பு
F(x)x = p(x ≤ x)
F(2) =\(\frac{1}{36}\)
F(4) = \(\frac{1}{36}\) + \(\frac{4}{36}\) = \(\frac{5}{36}\)
F(6) = \(\frac{1}{36}\) + \(\frac{4}{36}\) + \(\frac{10}{36}\) = \(\frac{15}{36}\) = \(\frac{5}{12}\)
F(8) = \(\frac{15}{36}\) + \(\frac{12}{36}\) = \(\frac{27}{36}\) = \(\frac{9}{12}\) = \(\frac{3}{14}\)
F(10) = \(\frac{27}{36}\) + \(\frac{9}{36}\) = \(\frac{36}{36}\) = 1
∵ குவிவு பரவல் சார்பு
F(x) = \(\left\{\begin{array}{ll}
0, & x<2 \\
\frac{5}{36}, & x \leq 2 \\
\frac{5}{12}, & x \leq 0 \\
\frac{3}{4}, & x \leq 8 \\
1, & x \leq 10
\end{array}\right.\)

(iii) p(4 ≤ x < 10) = p(x = 4) + p(x = 6) + p(x = 8)
= \(\frac{1}{9}\) + \(\frac{5}{18}\) + \(\frac{1}{2}\)
= \(\frac{2+5+6}{18}\) = \(\frac{13}{18}\)

(iv) p(r ≥ 6) = p(x = 6) + p(x = 8) + (p = 10)
= \(\frac{5}{18}\) + \(\frac{1}{3}\) + \(\frac{1}{4}\) = \(\frac{31}{36}\)

கேள்வி 3.
மகன் மற்றும் மகளுக்கு சமவாய்ப்பு நிகழ்தகவுகள் எனக் கருதி 4 குழந்தைகள் கொண்ட ஒரு குடும்பத்தில் உள்ள மகள்களின் எண்ணிக்கைக்கு நிகழ்தகவு நிறை சார்பினையும் குவிவு பரவல் சார்பினையும் காண்க.
தீர்வு:
கூறுவெளி = {4 குழந்தைகள்}
கொடுக்கப்பட்ட P(G) = P(B) = \(\frac{1}{2}\)
X குடும்பத்தில் உள்ள மகள்களின் எண்ணிக்கையை குறிக்கிறது என்க.
P(x = 0) = P(மகள் இல்லை)
= P(BBB) = \(\frac{1}{2}\) × \(\frac{1}{2}\) × \(\frac{1}{2}\) × \(\frac{1}{2}\)
= \(\frac{1}{16}\)

P(x = 1) = P(1 மகள்)
= 4C₁ × P = 4 × \(\frac{1}{16}\) = \(\frac{1}{4}\)
P(x = 2) = P(2 மகள்கள்)
= 4C₂ × P(GGBB)
= \(\frac{4 \times 3}{2 \times 1} \times \frac{1}{16}\) = \(\frac{3}{8}\)

P(x = 3) = P(3 மகள்கள்)
= 4C₃ × P(GGGB)
= 4 × \(\frac{1}{16}\) = \(\frac{1}{4}\)

P(x = 4) = P(4 மகள்கள்)
= P(GGGG) = \(\frac{1}{16}\)
நிகழ்தகவு நிறை சார்பு
f(x) = \(\left\{\begin{array}{ll}
\frac{1}{4}, & x=1,3 \\
\frac{1}{16}, & x=0,4 \\
\frac{3}{8}, & x=2
\end{array}\right.\)
குவிவு பரவல் சார்பு
F(0) = \(\frac{1}{16}\)
F(1) = \(\frac{1}{16}\) + \(\frac{1}{4}\) = \(\frac{5}{16}\)
F(2) = \(\frac{5}{16}\) + \(\frac{3}{8}\) = \(\frac{5}{16}\) + \(\frac{6}{16}\) = \(\frac{11}{16}\)
F(3) = \(\frac{11}{16}\) + \(\frac{1}{4}\) = \(\frac{11}{16}\) + \(\frac{4}{16}\) = \(\frac{15}{16}\)
F(4) = \(\frac{15}{16}\) + \(\frac{1}{16}\) = \(\frac{16}{16}\) = 1
F(x) = \(\left\{\begin{array}{ll}
\frac{0}{16}, & x<0 \\
\frac{1}{16}, & x \leq 0 \\
\frac{5}{16}, & x \leq 1 \\
\frac{11}{16}, & x \leq 2 \\
\frac{15}{16}, & x \leq 3 \\
1, & x \leq 4
\end{array}\right.\)

கேள்வி 4.
ஒரு தனிநிலை சமவாய்ப்பு மாறி 0, 1, மற்றும் 2 மதிப்புகளை மட்டுமே கொள்ளும் என்க.
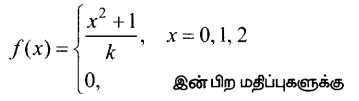
Samacheer Kalvi 12th Maths Guide Chapter 11 நிகழ்தகவு பரவல்கள் Ex 11.2 6
(i) k – இன் மதிப்பு
(ii) குவிவு பரவல் சார்பு
(iii) P(X ≥ 1) ஆகியவற்றைக் காண்க.
தீர்வு:
கொடுக்கப்பட்ட
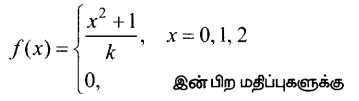
Samacheer Kalvi 12th Maths Guide Chapter 11 நிகழ்தகவு பரவல்கள் Ex 11.2 6
சமவாய்ப்பு மாறி X எடுத்துக் கொள்ளும் மதிப்புகள் 0, 1,2.
ஆதலால் f (x) நிகழ்தகவு நிறைச் சார்பு.
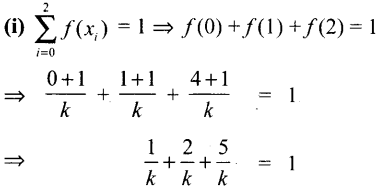
Samacheer Kalvi 12th Maths Guide Chapter 11 நிகழ்தகவு பரவல்கள் Ex 11.2 7
⇒ \(\frac{8}{k}\) = 1
⇒ k = 8
∵ f(x) = \(\frac{x^{2}+1}{k}\)
நிகழ்தகவு நிறைச் சார்பு

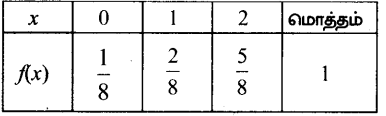
(ii)
F(0) = \(\frac{1}{8}\)
F(1) = \(\frac{1}{8}\) + \(\frac{2}{8}\) = \(\frac{3}{8}\)
F(2) = \(\frac{1}{8}\) + \(\frac{2}{8}\) + \(\frac{5}{8}\) = \(\frac{8}{8}\) = 1
குவிவு பரவல் சார்பு
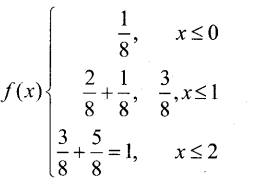
Samacheer Kalvi 12th Maths Guide Chapter 11 நிகழ்தகவு பரவல்கள் Ex 11.2 9

(iii) p(x ≥ 1) = p(x = 1) + p(x = 2) = \(\frac{2}{8}\) + \(\frac{5}{8}\)
p(x ≥ 1) = \(\frac{7}{8}\)

கேள்வி 5.
F(x) = \(\left\{\begin{array}{rr}
0 & -\infty<x<-1 \\
0.15 & -1 \leq x<0 \\
0.35 & 0 \leq x<1 \\
0.60 & 1 \leq x<2 \\
0.85 & 2 \leq x<3 \\
1 & 3 \leq x<\infty
\end{array}\right.\)
எனக்கொடுக்கப்பட்ட ஒருதனிநிலைசமவாய்ப்பு மாறியின் குவிவு சார்பிற்கு
(i) நிகழ்தகவு சார்பு
(ii) P(X ≥ 1) மற்றும்
(iii) P(X ≥ 2).
தீர்வு:
கொடுக்கப்பட்ட F(x) = \(\left\{\begin{array}{rr}
0 & -\infty<x<-1 \\
0.15 & -1 \leq x<0 \\
0.35 & 0 \leq x<1 \\
0.60 & 1 \leq x<2 \\
0.85 & 2 \leq x<3 \\
1 & 3 \leq x<\infty
\end{array}\right.\)
சமவாய்ப்பு மாறி X எடுத்துக்கொள்ளும் மதிப்புகள் -1, 0, 1,2,3
X என்ற தனிநிலை சமவாய்ப்பு மாறியிலிருந்து
f(x) = p(X = x)
∴ f(-1) = p(X = -1) = F(-1) – F(0)
= 0.15-0 = 0.15
f(0) = p(X = 0) = F(0) – F(-1)
0.35 -0.15 = 0.20
f(1) = p(X = 1) = F(1) – F(0)
0.60-0.35 = 0.25
f(2) = p(X = 2) = F(2) – F(1)
= 0.85-0.60 = 0.25
f(3) = p(X = 3) = F(3) – F(2)
= 1-0.85 = 0.15

(i) ∴ நிகழ்தகவு நிறைச் சார்பு
Samacheer Kalvi 12th Maths Guide Chapter 11 நிகழ்தகவு பரவல்கள் Ex 11.2 10

(ii) p(X < 1)
= p(X = -1) + p(X = 0) = 0.15 +0.20 = 0.35

(iii) p(X ≥ 2)
= p(X = 2) + p(X = 3) = 0.25 + 0.15 = 0.40

கேள்வி 6.
ஒரு சமவாய்ப்பு மாறி X-க்கு நிகழ்தகவு நிறை சார்பானது.
Samacheer Kalvi 12th Maths Guide Chapter 11 நிகழ்தகவு பரவல்கள் Ex 11.2 11
எனில்
(i) k மதிப்பு
(ii) P(2 ≤ X < 5)
(iii) P(3 < X) ஆகியவற்றைக் காண்க.
தீர்வு:
கொடுக்கப்பட்ட நிகழ்தகவு நிறைச் சார்பு
Samacheer Kalvi 12th Maths Guide Chapter 11 நிகழ்தகவு பரவல்கள் Ex 11.2 11
(i) f(x) நிகழ்தகவு நிறைச் சார்பு ஆதலால்
\(\sum_{i=1}^{5}\) f(x_i) = 1
⇒ k² + 2k² + 3k² + 2k + 3k = 1
⇒ 6k² + 5k = 1
⇒ 6k² + 5k – 1 =0
⇒ (k+ 1)(6k – 1) = 0
⇒ k=-1 அல்ல து k = \(\frac{1}{6}\) [∵ k = -1 என்பது சாத்தியமில்லை]
⇒ k = \(\frac{1}{6}\)

(ii) p(2 ≤ x < 5)
= p(x = 2) + p(x = 3) + p(x = 4)
= 2k² + 3k² + 2k = 5k² + 2k
= 5(\(\frac{1}{36}\)) + 2(\(\frac{1}{6}\)) = \(\frac{5}{36}\) + \(\frac{1}{3}\) = \(\frac{5+12}{36}\) = \(\frac{17}{36}\)

(iii) p(3 < x) = p(x > 3)
= p(x = 4) + p(x = 5) = 2k + 3k = 5k
= 5(\(\frac{1}{6}\)) = \(\frac{5}{6}\)

கேள்வி 7.
F(x) = Samacheer Kalvi 12th Maths Guide Chapter 11 நிகழ்தகவு பரவல்கள் Ex 11.2 13
என்பது ஒரு தனிநிலை – சமவாய்ப்பு மாறியின் குவிவு பரவல் சார்பு எனில்
(i) நிகழ்தகவு நிறை சார்பு
(ii) P(X < 3) மற்றும்
(iii) P(X = 2).
தீர்வு:
கொடுக்கப்பு f(x) = Samacheer Kalvi 12th Maths Guide Chapter 11 நிகழ்தகவு பரவல்கள் Ex 11.2 13

(i) சமவாய்ப்பு மாறி X எடுத்துக் கொள்ளும் மதிப்புகள் 0, 1, 2, 3, 4.
தனிநிலை சமவாய்ப்பு மாறிக்கு நம்மிடம்
f(x) = p(X = x)
∴ f(0) = F(0) = \(\frac{1}{2}\)
f(1) = F(1) – F(0)
= \(\frac{3}{5}\) – \(\frac{5}{6}\) = \(\frac{6-5}{10}\) = \(\frac{1}{10}\)

f(2) = F(2) – F(1)
= \(\frac{4}{5}\) – \(\frac{3}{5}\) = \(\frac{1}{5}\)

f(3) = F(3) – F(2)
= \(\frac{9}{10}\) – \(\frac{4}{5}\) = \(\frac{9-8}{10}\) = \(\frac{1}{10}\)

f(4) = F(4) – F(3)
= 1 – \(\frac{9}{10}\) = \(\frac{1}{10}\)
∴ நிகழ்தகவு நிறைச் சார்பு
Samacheer Kalvi 12th Maths Guide Chapter 11 நிகழ்தகவு பரவல்கள் Ex 11.2 14