Samacheer Kalvi 12th Business Maths Solutions Chapter 9 Applied Statistics Additional Problems

Students can download 12th Business Maths Chapter 9 Applied Statistics Additional Problems and Answers, Samacheer Kalvi 12th Business Maths Book Solutions Guide Pdf helps you to revise the complete Tamilnadu State Board New Syllabus and score more marks in your examinations.

Tamilnadu Samacheer Kalvi 12th Business Maths Solutions Chapter 9 Applied Statistics Additional Problems

Choose the correct answer.

Question 1.
Match the following.

(a) Seasonal variation	(i) Erratic variation
(b) Secular trend	(ii) Business cycle
(c) Irregular variation	(iii) Long time variation
(d) Cyclical variation	(iv) Short time variation

Answer:
(a) – (iv)
(b) – (iii)
(c) – (i)
(d) – (ii)

Question 2.
The secular trend can be measure by ______
(a) 4 methods
(b) 1 method
(c) 2 methods
(d) none of these
Answer:
(a) 4 methods

Question 3.
Method of simple averages is used to measure _________
(a) Secular trend
(b) Irregular variation
(c) Seasonal variation
(d) Cyclic variation
Answer:
(c) Seasonal variation

Question 4.
Increase in the number of patients in the hospital due to heatstroke is _______
(a) Secular trend
(b) Irregular variation
(c) Seasonal variation
(d) Cyclic variation
Answer:
(c) Seasonal variation

Question 5.
In time series seasonal variations can occur within a period of ________
(a) 4 years
(b) 3 years
(c) one year
(d) 9 years
Answer:
(c) one year

Question 6.
Fill in the blanks.

1. The method of moving averages is used to find the _________
2. Most frequently used mathematical model of a time series is _________
3. The sale of air condition increases during summer is a ________
4. The fire in a factory is an example of ________
5. The best-fitting trend is one in which the sum of squares of residuals is _______

Answer:

1. Secular trend
2. Multiplicative model
3. Seasonal variation
4. Irregular variation
5. Least

Question 7.
True or False

1. An index number is used to measure changes in a variable over time.
2. The ratio of a new price to the base year price is called the price relative.
3. The Laspeyre’s and Paasche index numbers are examples of weighted quantity index only.
4. \(\frac{\sum p_{1} q_{1}}{\sum p_{0} q_{1}} \times 100\) is Laspeyre’s quantity index.
5. Laspeyre’s price index regards the base year quantities as fixed.

Answer:

1. True
2. True
3. False
4. False
5. True

Question 8.
Index for base period is always taken as ______
(a) 100
(b) 1
(c) 200
(d) 0
Answer:
(a) 100

Question 9.
Consumer price index indicates _______
(a) Rise
(b) Fall
(c) both (a) & (b)
(d) neither (a) & (b)
Answer:
(c) both (a) & (b)

Question 10.
The purchasing power of money can be accessed through ______
(a) simple index
(b) Fisher’s index
(c) Consumer price index (CPI)
(d) Volume index
Answer:
(c) Consumer price index (CPI)

Question 11.
For consumer price index, price quotations are collected from _______
(a) Fair price shops
(b) Government depots
(c) Retailers
(d) Whole-sale dealers
Answer:
(c) Retailers

Question 12.
The aggregative expenditure method and family budget method always give ________
(a) Different results
(b) Approximate results
(c) Same results
(d) None of these
Answer:
(c) Same results

Question 13.
The Federal Bureau of statistics prepares ________
(a) The wholesale price index
(b) CPI
(c) Sensitive price indicator
(d) All the above
Answer:
(d) All the above

Question 14.
Paasche’s price index number is also called _________
(a) Base year weighted
(b) Current year weighted
(c) Simple aggregative index
(d) Consumer price index
Answer:
(b) Current year weighted

Question 15.
Index number calculated by Fisher’s formula is ideal because it satisfies ________
(a) Circular test
(b) Factor reversal test
(c) Time reversal test
(d) All of the above
Answer:
(d) All of the above

2 Mark Questions

Question 1.
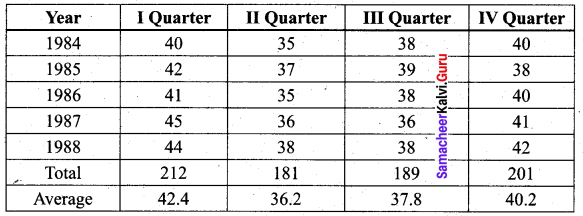
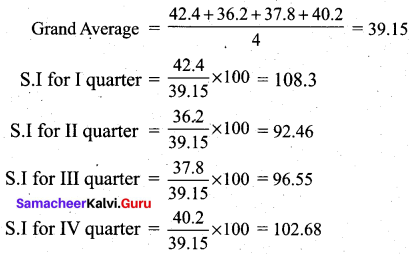
From the data given below calculate seasonal Indices:

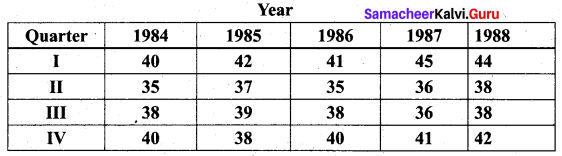
Solution:

Question 2.
Using 3-year moving averages, determine the trend values from the following data.

Solution:

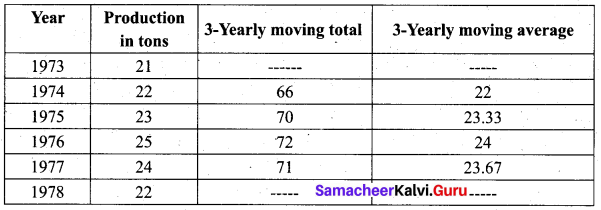
Question 3.
A company estimates its average monthly sales in a particular year to be Rs.2,00,000. The seasonal indices of the sales data are given below. Draw a monthly sales budget for the company.

Solution:

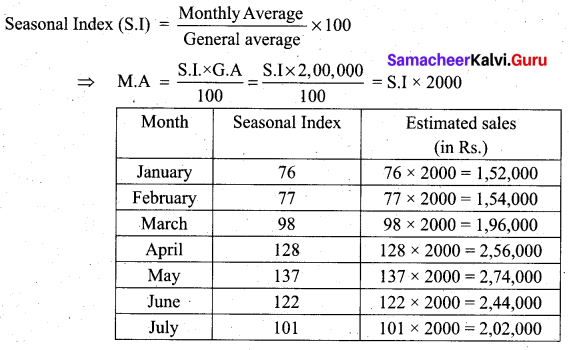
Question 4.
Calculate the index for the data when the average percentage increases in the prices of items and weights are given. Food 15, clothing 3, Rent 4, Fuel 2, Miscellaneous 1, the percentage increases are 32, 54, 47, 78 and 58.
Solution:

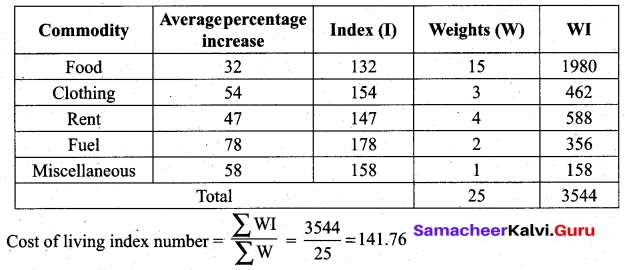
3 and 5 Marks Questions

Question 1.
Using Fisher’s Ideal Formula, compute price and quantity index number for 1984 with 1982 as the base year, from the given information.

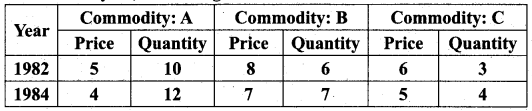
Solution:

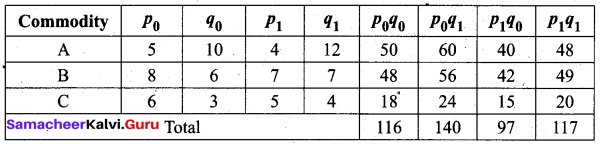
Question 2.
Using the following data, compute Fisher’s Ideal price index number for the current year.

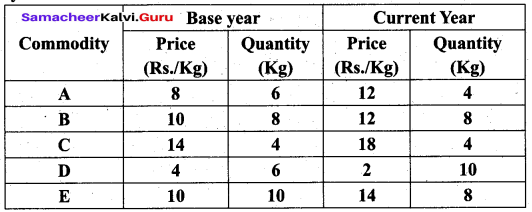
Solution:

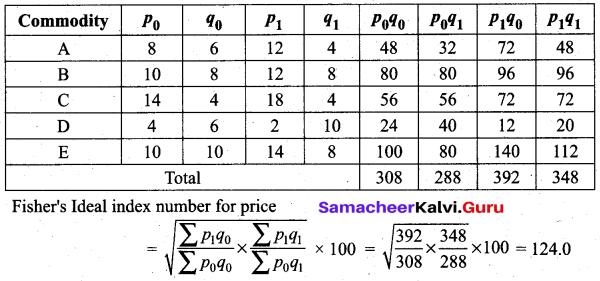
Question 3.
Calculate the cost of living Index number from the following data.

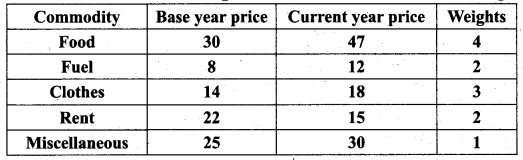
Solution:

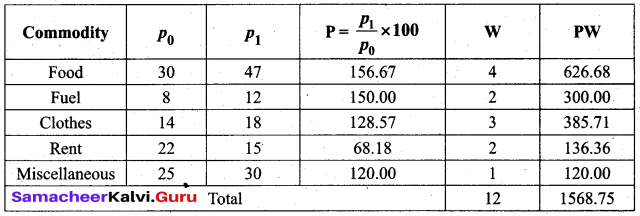
Cost of living index number = \(\frac{\sum P W}{\sum W}=\frac{1568.75}{12}\) = 130.73

Question 4.
Given below are the values of the sample mean (\(\bar{X}\)) and the range (R) for ten samples of size 5 each. Find the control charts and comment on the state of the process.

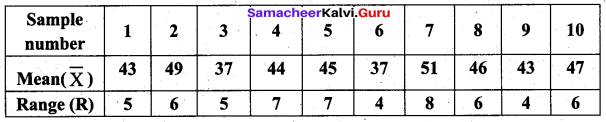
Use A₂ = 0.58, D₃ = 0, D₄ = 2.115
Solution:


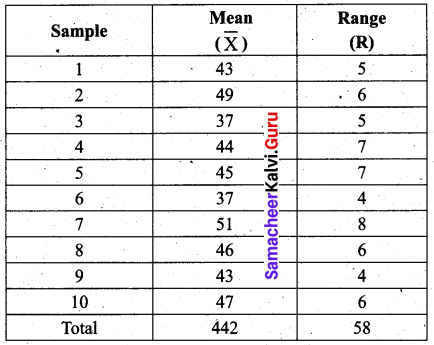
We observe that all the sample range values are within the control limits values of R chart, But two values of the sample \(\bar{X}\) (i.e) 37, 37 lies below the LCL and 49, 51 lie above the UCL. So the statistical process is out of control.

Question 5.
Fit a straight line trend equation by the method of least squares and estimate the trend values.

Solution:
Let Y_t = a + bx be the trend line.
Let X = \(\frac{x-1964.5}{0.5}\), x denotes year.

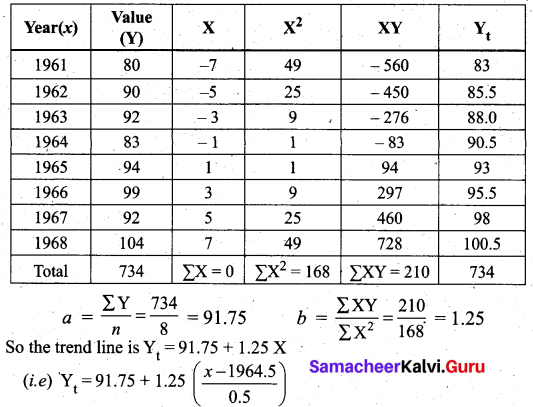
When x = 1961, Y_t = 91.75 – 7(1.25) = 83
When x = 1962, Y_t = 91.75 – 5(1.25) = 85.5
We can find other values similarly.