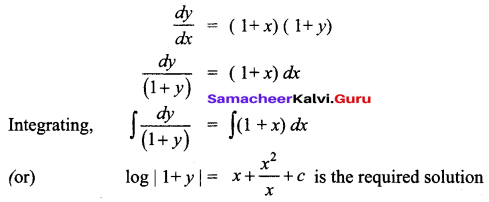Students can download 12th Business Maths Chapter 4 Differential Equations Miscellaneous Problems and Answers, Samacheer Kalvi 12th Business Maths Book Solutions Guide Pdf helps you to revise the complete Tamilnadu State Board New Syllabus and score more marks in your examinations.
Tamilnadu Samacheer Kalvi 12th Business Maths Solutions Chapter 4 Differential Equations Miscellaneous Problems
Question 1.
Suppose that Qd = 30 – 5P + 2 \(\frac{d p}{d t}+\frac{d^{2} p}{d t^{2}}\) and Qs = 6 + 3P. Find the equilibrium price for market clearance.
Solution:
For equilibrium price Qd = Qs
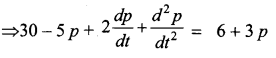

Question 2.
Form the differential equation having for its general solution y = ax2 + bx
Solution:
Given y = ax2 + bx
Since there are 2 constants a, b we have to differentiate twice to eliminate them


Question 3.
Solve yx2 dx + e-x dy = 0
Solution:
The given equation can be written as

Question 4.
Solve: (x2 + y2) dx + 2xy dy = 0
Solution:
The given equation can be written as \(\frac{d y}{d x}=-\frac{\left(x^{2}+y^{2}\right)}{2 x y}\)
It is a homogeneous differential equation


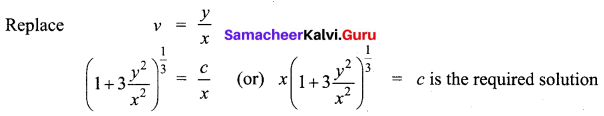
Question 5.
Solve: x \(\frac{d y}{d x}\) + 2y = x4
Solution:

Question 6.
A manufacturing company has found that the cost C of operating and maintaining the equipment is related to the length ‘m’ of intervals between overhauls by the equation \(m^{2} \frac{d C}{d m}\) + 2mC = 2 and c = 4 and when m = 2. Find the relationship between C and m.
Solution:

given that c = 4 when m = 2
4(4) = 2(2) + k
k = 12
So the relation ship between C and m is Cm2 = 2m + 12 = 2(m + 6)
Question 7.
Solve (D2 – 3D + 2)y = e4x given y = 0 when x = 0 and x = 1.
Solution:
(D2 – 3D + 2)y = e4x
The auxiliary equations is m2 – 3m + 2 = 0
(m – 2) (m – 1) = 0
m = 2, 1



Question 8.
Solve: \(\frac{d y}{d x}\) + y cos x = 2cos x
Solution:
The given equation can be written as \(\frac{d y}{d x}\) + (cos x)y = 2 cos x
It is of the form \(\frac{d y}{d x}\) + Py = Q
Where P = cos x, Q = 2 cos x
Now ∫Pdx = ∫cos x dx = sin x
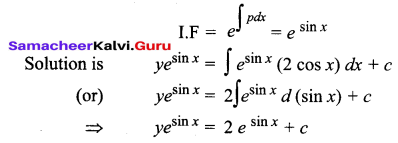
Question 9.
Solve: x2y dx – (x3 + y3) dy = 0
Solution:


Question 10.
Solve: \(\frac{d y}{d x}\) = xy + x + y + 1
Solution: