Samacheer Kalvi 12th Business Maths Solutions Chapter 4 Differential Equations Ex 4.4

Students can download 12th Business Maths Chapter 4 Differential Equations Ex 4.4 Questions and Answers, Samacheer Kalvi 12th Business Maths Book Solutions Guide Pdf helps you to revise the complete Tamilnadu State Board New Syllabus and score more marks in your examinations.

Tamilnadu Samacheer Kalvi 12th Business Maths Solutions Chapter 4 Differential Equations Ex 4.4

Solve the following:

Question 1.
\(\frac{d y}{d x}-\frac{y}{x}=x\)
Solution:

Question 2.
\(\frac{d y}{d x}\) + y cos x = sin x cos x
Solution:
The given equation can be written as \(\frac{d y}{d x}\) + (cos x) y = sin x cos x
It is of the form \(\frac{d y}{d x}\) + Py = Q dx
Here P = cos x, Q = sin x cos x
∫P dx = ∫cos x dx = sin x

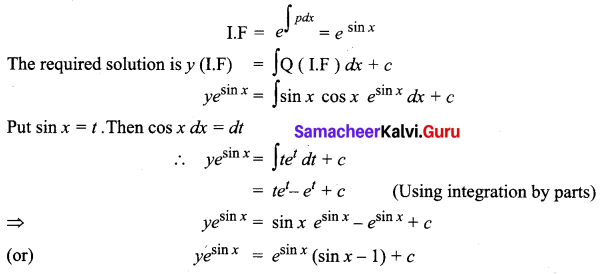
Question 3.
x \(\frac{d y}{d x}\) + 2y = x⁴
Solution:
The given equation can be written as \(\frac{d y}{d x}+\frac{2}{x} y=x^{3}\)

Question 4.
\(\frac{d y}{d x}+\frac{3 x^{2}}{1+x^{3}} y=\frac{1+x^{2}}{1+x^{3}}\)
Solution:
The given equation is of the form \(\frac{d y}{d x}\) + Py = Q

Question 5.
\(\frac{d y}{d x}+\frac{y}{x}=x e^{x}\)
Solution:
The given equation is of the form \(\frac{d y}{d x}\) + Py = Q

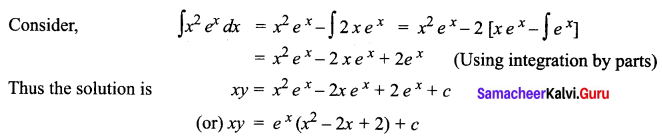
Question 6.
\(\frac{d y}{d x}\) + y tan x = cos³ x
Solution:
The given equation is of the form \(\frac{d y}{d x}\) + Py = Q
where P = tan x, Q = cos³ x
Now ∫P dx = ∫tan x dx = log sec x

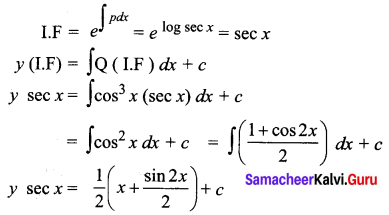
Question 7.
If \(\frac{d y}{d x}\) + 2y tan x = sin x and if y = 0 when x = \(\frac{\pi}{3}\) express y in terms of x
Solution:
\(\frac{d y}{d x}\) + 2y tan x = sin x
Here P = 2 tan x and Q = sin x
∫P dx = ∫2 tan x = 2 log sec x = log sec² x

c = -sec\(\frac{\pi}{3}\) = -2
The solution is y sec² x = sec x – 2

Question 8.
\(\frac{d y}{d x}+\frac{y}{x}=x e^{x}\)
Solution:

Question 9.
A bank pays interest by continuous compounding, that is by treating the interest rate as the instantaneous rate of change of principal. A man invests ₹ 1,00,000 in the bank deposit which accrues interest, 8% per year compounded continuously. How much will he get after 10 years? (e^0.8 = 2.2255)
Solution:
Let P be the principal at time ‘t’
According to the given condition,

The man will get ₹ 2,22,550 after 10 years.