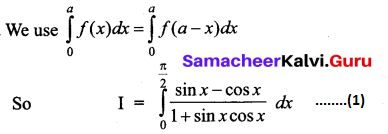Students can download 12th Business Maths Chapter 2 Integral Calculus I Additional Problems and Answers, Samacheer Kalvi 12th Business Maths Book Solutions Guide Pdf helps you to revise the complete Tamilnadu State Board New Syllabus and score more marks in your examinations.
Tamilnadu Samacheer Kalvi 12th Business Maths Solutions Chapter 2 Integral Calculus I Additional Problems
I. One Mark Questions
Choose the correct answer.
Question 1.
The integral of \(\left(\sqrt{x}+\frac{1}{\sqrt{x}}\right)\) equals _____

Answer:
(c) \(\frac{2}{3} x^{\frac{3}{2}}+2 x^{\frac{1}{2}}+c\)
Question 2.
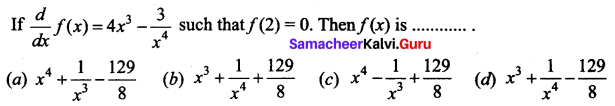
Answer:
(a) \(x^{4}+\frac{1}{x^{3}}-\frac{129}{8}\)
Hint:

Question 3.
\(\int \frac{\sin ^{2} x-\cos ^{2} x}{\sin ^{2} x \cos ^{2} x} d x\) is equal to _____
(a) tan x + cot x + c
(b) tan x + cosec x + c
(c) -tan x + cot x + c
(d) tan x – sec x + c
Answer:
(a) tan x + cot x + c
Hint:
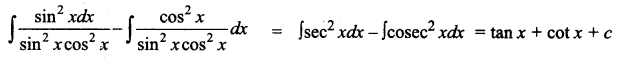
Question 4.

Answer:
(d) \(\frac{\pi}{12}\)
Hint:
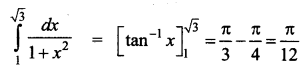
Question 5.
The value of \(\int_{-\frac{\pi}{2}}^{\frac{\pi}{2}}\left(x^{3}+x \cos x+\tan ^{5} x\right) d x\) is ______
(a) 0
(b) 2
(c) π
(d) 1
Answer:
(a) 0
Hint:
Let f(x) = x3 + x cos x + tan5 x
f(-x)= -x3 – x cos x – tan5 x = -f(x)
So f(x) is odd function.
Integral is 0.
Question 6.
Fill in the blanks.
(a) \(\int_{0}^{\frac{\pi}{2}} \cos ^{3} x d x\) is equal to _____
(b) \(\int_{-\frac{\pi}{2}}^{\frac{\pi}{2}} \sin ^{31} x d x\) is equal to _________
Answer:
(a) \(\frac{2}{3}\)
(b) 0
Hint:
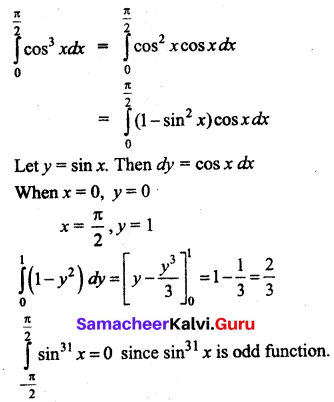
Question 7.
Match the following.


Answer:
(a) – (iii)
(b) – (iv)
(c) – (v)
(d) – (ii)
(e) – (i)
Question 8.
State True or False.
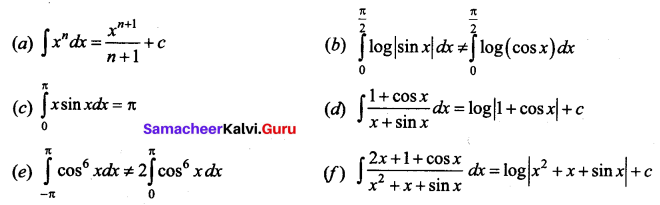
Answer:
(a) True
(b) False
(c) True
(d) False
(e) False
(f) True
Question 9.
Which of the following is not equal to ∫ tan x sec2 x dx?
(a) \(\frac{1}{2} \tan ^{2} x\)
(b) \(\frac{1}{2} \sec ^{2} x\)
(c) \(\frac{1}{2 \cos ^{2} x}\)
(d) None of these
Answer:
(d) None of these
Hint:

Question 10.
∫ex (cos x – sin x) dx is equal to ______
(a) ex sin x + c
(b) ex cos x + c
(c) -ex cos x + c
(d) -ex sin x + c
Answer:
(b) ex cos x + c
Hint:
Let f(x) = cos x
f'(x) = -sin x
∫ex [f(x) + f'(x)] dx = ex f(x) + c
Question 11.
\(\int \frac{1-\cos 2 x}{1+\cos 2 x} d x\) is _____
(a) tan x – x + c
(b) x + tan x + c
(c) x – tan x + c
(d) -x – cot x + c
Answer:
(a) tan x – x + c
Hint:
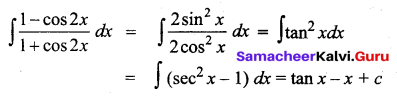
Question 12.
\(\int_{0}^{\frac{\pi}{2}} \cos x e^{\sin x} d x\) is equal to ______
(a) e = 1
(b) 1 – e
(c) \(e^{\frac{\pi}{2}}-1\)
(d) \(1-e^{\frac{\pi}{2}}\)
Answer:
(a) e = 1
Hint:

Question 13.
Which of the following is an even function?
(a) sin x
(b) ex – e-x
(c) x cos x
(d) cos x
Answer:
(d) cos x
Question 14.
Which of the following is neither odd nor even function?
(a) x sin x
(b) x2
(c) e-x
(d) x cos x
Answer:
(c) e-x
Question 15.
∫sec2 (7 – 4x) dx equal to ______
(a) tan (7 – 4x)
(b) -tan (7 – 4x)
(c) –\(\frac{1}{4}\) tan (7 – 4x)
(d) \(\frac{1}{4}\) tan (7 – 4x)
Answer:
(c) – \(\frac{1}{4}\) tan (7 – 4x)
II. 2 Mark Questions.
Question 1.
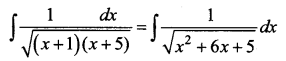
Solution:
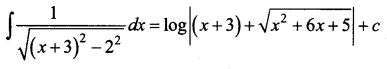
Question 2.
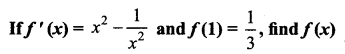
Answer:
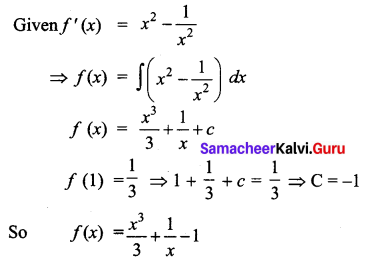
Question 3.
\(\int\left(e^{x}+e^{-x}\right)^{2} d x\)
Solution:
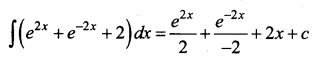
Question 4.
Find \(\int x^{5} \sqrt{3+5 x^{6}} d x\)
Solution:
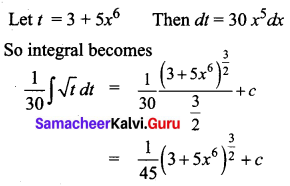
Question 5.
\(\int \frac{(x+1)(x+\log x)^{2}}{x} d x\)
Solution:
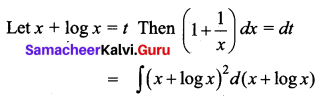
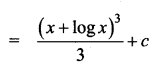
Question 6.
\(\int \frac{e^{2 x}-1}{e^{2 x}+1} d x\)
Solution:
Dividing numerator and denominator by ex, we get \(\int \frac{e^{x}-e^{-x}}{e^{x}+e^{-x}} d x\)
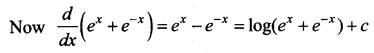
Question 7.
\(\int \frac{1}{x+\sqrt{x}} d x\)
Solution:

III. 3 and 5 Mark Questions.
Question 1.
Find \(\int \frac{e^{x}(x+1)}{(x+3)^{3}} d x\)
Solution:

Question 2.
\(\int \frac{1}{2 x^{2}-x-1} d x\)
Solution:

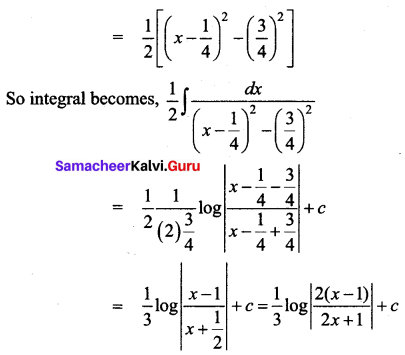
Question 3.
\(\int \frac{1}{1-3 \sin ^{2} x} d x\)
Solution:
Divide the numerator and denominator by cos2 x
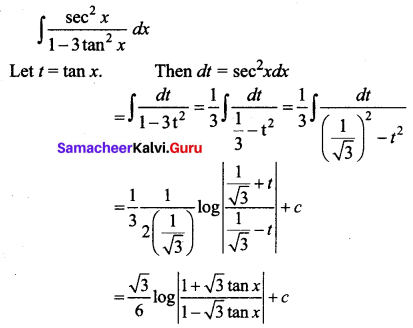
Question 4.
\(\int \frac{d x}{e^{x}-e^{-x}}\)
Solution:
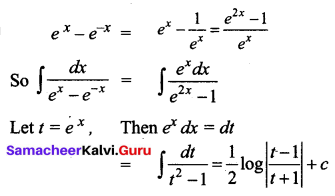
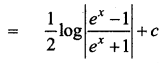
Question 5.
Evaluate \(\int_{-1}^{2}(7 x-5) d x\) as the limit of a sum.
Solution:

Question 6.
Evaluate \(\int_{1}^{2}\left(x^{2}-1\right) d x\) as the limit of a sum.
Solution:

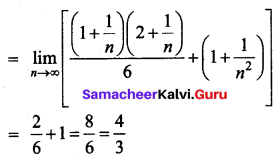
Question 7.
Evaluate \(\int_{1}^{2} \frac{1}{x\left(x^{4}+1\right)} d x\)
Solution:

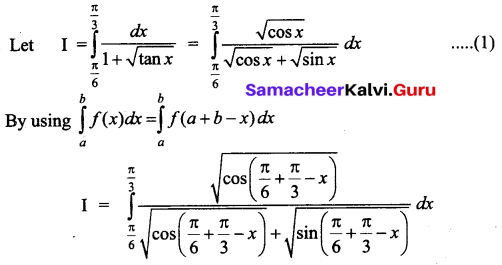
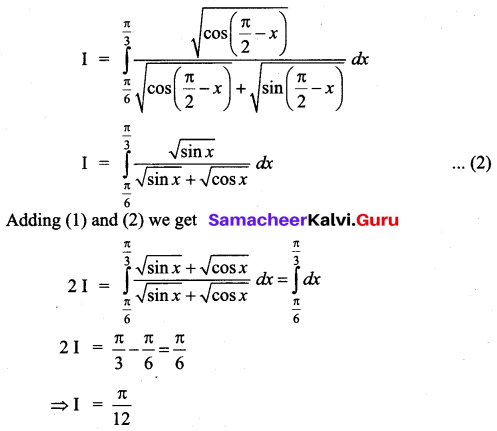
Question 8.
Evaluate \(\int_{\frac{\pi}{6}}^{\frac{\pi}{3}} \frac{d x}{1+\sqrt{\tan x}}\)
Solution:
Question 9.
Evaluate \(\int_{0}^{1} x(1-x)^{5} d x\)
Solution:

Question 10.
Evaluate \(\int \frac{2 x+3}{\sqrt{x^{2}+x+1}} d x\)
Solution:
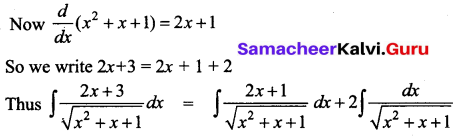
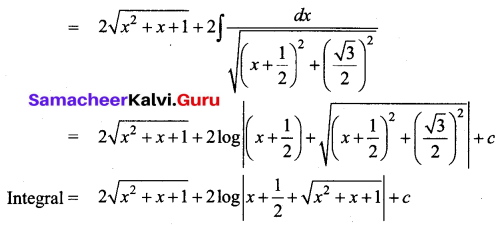
Question 11.
∫(x2 + 1) log x dx
Solution:

Question 12.
\(\int \sqrt{x^{2}+4 x-5} d x\)
Solution:
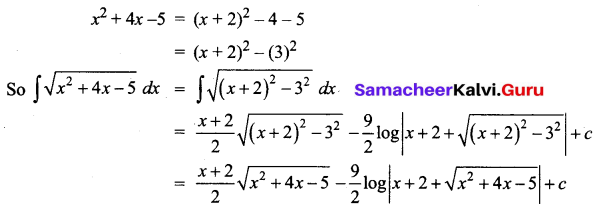
Question 13.
\(\int_{0}^{\frac{\pi}{4}}\left(2 \sec ^{2} x+x^{3}+2\right) d x\)
Solution:
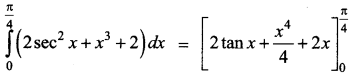
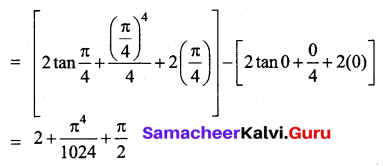
Question 14.
Evaluate \(\int_{0}^{1} \frac{2 x}{\left(x^{2}+1\right)\left(x^{2}+2\right)} d x\)
Solution:
Let x2 = t, then 2x dx = dt
when x = 0, t = 0 and x = 1, t = 1
so integral becomes, \(\int_{0}^{1} \frac{d t}{(t+1)(t+2)}\)
We use partial fractions to proceed further
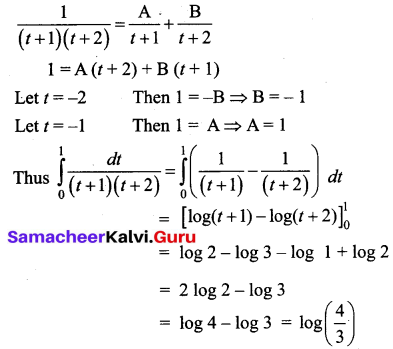
Question 15.
\(\int_{0}^{\frac{\pi}{2}} \frac{\sin x-\cos x}{1+\sin x \cos x} d x\)
Solution: