Students can Download Computer Applications Chapter 2 Number Systems Questions and Answers, Notes Pdf, Samacheer Kalvi 11th Computer Applications Book Solutions Guide Pdf helps you to revise the complete Tamilnadu State Board New Syllabus and score more marks in your examinations.
Tamilnadu Samacheer Kalvi 11th Computer Applications Solutions Chapter 2 Number Systems
Samacheer Kalvi 11th Computer Applications Number Systems Text Book Back Questions and Answers
I. Choose The Correct Answer
Question 1.
Which refers to the number of bits processed by a computer’s CPU?
(a) Byte
(b) Nibble
(c) Word length
(d) Bit
Answer:
(c) Word length
![]()
Question 2.
How many bytes does 1 KiloByte contain?
(a) 1000
(b) 8
(c) 4
(d) 1024
Answer:
(d) 1024
Question 3.
Expansion for ASCII:
(a) American School Code for Information Interchange
(b) American Standard Code for Information Interchange
(c) All Standard Code for Information Interchange
(d) American Society Code for Information Interchange
Answer:
(b) American Standard Code for Information Interchange
![]()
Question 4.
2^50 is referred as:
(a) kilo
(b) tera
(c) peta
(d) zetta
Answer:
(c) peta
Question 5.
How many characters can be handled in Binary Coded Decimal System?
(a) 64
(b) 255
(c) 256
(d) 128
Answer:
(a) 64
Question 6.
For 11012 what is the Hexadecimal equivalent?
(a) F
(b) E
(c) D
(d) B
Answer:
(c) D
![]()
Question 7.
What is the 1 ’s complement of 00100110?
(a) 00100110
(b) 11011001
(c) 11010001
(d) 00101001
Answer:
(b) 11011001
![]()
Question 8.
Which amongst this is not an Octal number?
(a) 645
(b) 234
(c) 876
(d) 123
Answer:
(c) 876
II. Short Answers
Question 1.
What is data?
Answer:
The term data comes from the word datum, which means a raw fact. The data is a fact about people, places or some objects.
Eg: Let ‘Name’, ‘Age’, ‘Class’, ‘Marks’ and ‘Subject’ be some defined variables. Now, let us assign a value to each of these variables.
Name = Rajesh
Age = 16
Class = XI
Mark – 65
Subject = Computer Science
In the above example, the values assigned to the five different variables are called data.
![]()
Question 2.
Write the l’s complement procedure?
Answer:
- Step 1: Convert given Decimal number into Binary
- Step 2: Check if the binary number contains 8 bits, if less add 0 at the left most bit, to make it as 8 bits.
- Step 3: Invert all bits (i.e. Change 1 as 0 and 0 as 1)
Question 3.
Convert (46)10 into Binary number?
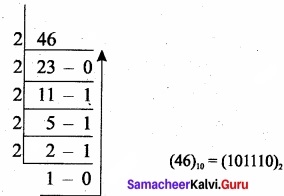
Question 4.
We cannot find 1’s complement for (28)10. State reason?
Answer:
1’s complement representation is an easier approach to represent signed numbers. This is for negative numbers only. This (28)10 this whole numbers cannot be determined by negative number because the number whose MSB is 1.
![]()
Question 5.
List the encoding systems for characters immemory?
Answer:
There are several encoding systems used for computer. They are
- BCD: Binary Coded Decimal.
- EBCDIC: Extended Binary Coded Decimal Interchange Code.
- ASCII: American Standard Code for Information Interchange.
- Unicode
- ISCII: Indian Standard Code for Information Interchange.
III. Explain in Brief
Question 1.
What is radix of a number system? Give example?
Answer:
A numbering system is a way of representing numbers. The most commonly used numbering system in real life is Decimal number system. Other number systems are Binary, Octal, Hexadecimal number system. Each number system is uniquely identified by its base value or radix. Radix or base is the count of number of digits in each number system. Radix or base is the general idea behind positional numbering system.
Eg: (123)10, (547)g, (1001)2, (25)16.
![]()
Question 2.
Write note on binary number system?
Answer:
There are only two digits in the Binary system, namely, 0 and 1. The numbers in the binary system are represented to the base 2 and the positional multipliers are the powers of 2. The left most bit in the binary number is called as the Most Significant Bit (MSB) and it has the largest positional weight. The right most bit is the Least Significant Bit (LSB) and has the smallest positional weight.
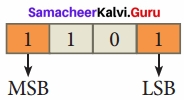
Eg: The binary sequence (1101)2 has the decimal equivalent:
(1101)2 = 1 × 23+ 1 × 22 + 0 × 21 + 1 × 20
= 8 + 4 + 0+ 1 = (13)10
Question 3.
Convert (150)10 into Binary, then convert that Binary number to Octal?
Binary number:

Binary number to octal:

Question 4.
Write short note on ISCII?
Answer:
ISCII is the system of handling the character of Indian local languages. This as a 8-bit coding system. Therefore it can handle 256 (2s) characters. This system is formulated by the department of Electronics in India in the year 1986-88 and recognized by Bureau of Indian Standards (BIS). Now this coding system is integrated with Unicode.
![]()
Question 5.
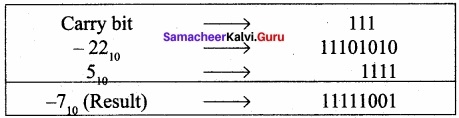
Add:
(i)-2210+1510
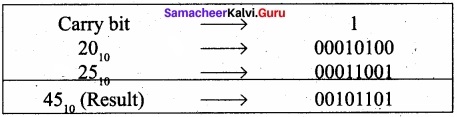
(ii) 2010+ 2510
Answer:
(i) -22 +15
The binary equivalent of 22 is 00010110

The binary equivalent of 15 is 1111.
Binary addition of -22 and +15
(ii) 20 + 25
Binary number for 20 = 00010100
Binary number or 25 = 00011001
IV. Explain in detail.
Question 1.
(a) Write the procedure to convert fractional Decimal to Binary.
(b) Convert (98.46)10 to Binary.
Answer:
(a) The method of repeated multiplication by 2 has to be used to convert such kind of decimal fractions.
The steps involved in the method of repeated multiplication by 2:
Step 1: Multiply the decimal fraction by 2 and note the integer part. The integer part is either 0 or 1.
Step 2: Discard, the integer part of the previous product. Multiply the fractional part of the previous product by 2 Repeat Step 1 until the same fraction repeats or terminates (0).
Step 3: The resulting integer part forms a sequence of Os and Is that become the binary equivalent of decimal fraction.
Step 4: The final answer is to be written from first integer part obtained till the last integer part obtained.
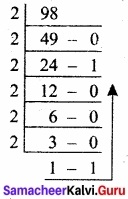

(98.46)10 = (1100010.011101011…..)2
![]()
Question 2.
Find 1’s Complement and 2’s Complement for the following Decimal number:
(a) – 98
(b) -135
(a) – 98
First convert given decimal number into binary:
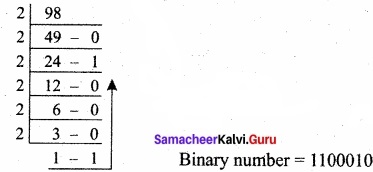
Binary number = 1100010
Binary number = 1100010
Second, check binary number as 8 bits, If less add 0 as the left most bit, 01100010
Third, Invert all bits (change 1 as 0 and 0 as 1)
1’s complement for 10011101.
2’s complement:

(b) – 135
First convert gives decimal number into Binary.

Binary number = 10000111
Second, check binary number as 8 bits, If less add 0 at the left most bit. It has 8 bits, 10000111.
Third, Invert all bits (change 1 as 0 and 0 as 1)
1 ’s complement for 01111000.
2’s complement:

2’s complement of – 135 – 01111001
![]()
Question 3.
(a) Add 11010102+ 1011012
(b) Subtract 11010112 – 11101022
Answer:
(a) 11010102 + 1011012
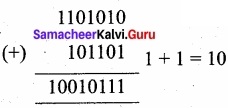
11010102 + 1011012 = 100101112
(b) 11010112 – 1110102
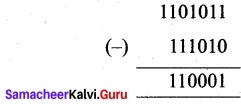
11010112 – 1110102 = 1100012
Samacheer Kalvi 11th Computer Applications Number Systems Additional Questions and Answers
I. Choose The Correct Answer
Question 1.
A bit is the short form of:
(a) binary data
(b) binary digit
(c) binary decimal
(d) big digit
Answer:
(b) binary digit
![]()
Question 2.
A ……………………… is a collection of 4 bits.
(a) bit
(b) byte
(c) nibble
(d) word length
Answer:
(c) nibble
Question 3.
A collection of 8 bits is called:
(a) bit
(b) byte
(c) word length
(d) nibble
Answer:
(b) byte
![]()
Question 4.
2^40 is referred as:
(a) mega
(b) giga
(c) peta
(d) tera
Answer:
(d) tera
Question 5.
2^70 is referred as:
(a) peta
(b) exa
(c) zetta
(d) yotta
Answer:
(c) zetta
![]()
Question 6.
1024 GB is referred as:
(a) kilo byte
(b) mega byte
(c) giga byte
(d) tera byte
Answer:
(d) tera byte
Question 7.
……………………. are used to represent characters in a text.
(a) Bits
(b) Bytes
(c) Nibble
(d) Wordlength
Answer:
(b) Bytes
![]()
Question 8.
The ASCII value for blank space is:
(a) 32
(b) 91
(c) 48
(d) 65
Answer:
(a) 32
Question 9.
The ASCII value for numeric 0 is:
(a) 32
(b) 91
(c) 48
(d) 65
Answer:
(c) 48
![]()
Question 10.
Each number system is uniquely identified by its:
(a) decimal value
(b) binary value
(c) base value or radix
(d) octal value
Answer:
(c) base value or radix
Question 11.
The range of ASCII values for lower case alphabets is from:
(a) 97 to 122
(b) 65 to 90
(c) 98 to 122
(d) 97 to 123
Answer:
(a) 97 to 122
![]()
Question 12.
The range of ASCII values for upper case alphabets is from:
(a) 97 to 122
(b) 65 to 90
(c) 66 to 90
(d) 65 to 97
Answer:
(b) 65 to 90
Question 13.
The expansion of MSB is:
(a) most significant bit
(b) most signed bit
(c) must significant bit
(d) must signed bit
Answer:
(a) most significant bit
Question 14.
The expansion of LSB is:
(a) lower significant bit
(b) least significant bit
(c) lower signed bit
(d) least signed bit
Answer:
(b) least significant bit
![]()
Question 15.
Radix of octal number is:
(a) 2
(b) 10
(c) 16
(d) 1
Answer:
(d) 1
Question 16.
The binary sequence (1101 )2 has the decimal equivalent:
(a) (25)10
(b) ( 15)10
(c) (17)10
(d) (13)10
Answer:
(d) (13)10
Question 17.
In hexadecimal C represents:
(a) 11
(b) 0
(c) 12
(d) 15
Answer:
(c) 12
![]()
Question 18.
The simplest method to represent negative binary numbers is called:
(a) signed magnitude
(b) unsigned magnitude
(c) magnitude bit
(d) unmagnitude bit
Answer:
(a) signed magnitude
Question 19.
EBDIC coding system can handle …………………….. characters.
(a) 64
(b) 255
(c) 256
(d) 128
Answer:
(c) 256
![]()
Question 20.
The most commonly used coding scheme is the:
(a) Binary Coded Decimal
(b) Extended Binary Coded Decimal Interchange Code
(c) Indian Standard Code for Information Interchange
(d) American Standard Code for Information Interchange
Answer:
(d) American Standard Code for Information Interchange
II. Short Answers
Question 1.
Define word length?
Answer:
Word length refers to the number of bits processed by a Computer’s CPU. For example, a word length can have 8 bits, 16 bits, 32 bits and 64 bits (Present day Computers use 32 bits or 64 bits).
![]()
Question 2.
Define byte?
Answer:
A collection of 8 bits is called Byte. A byte is considered as the basic unit of measuring the memory size in the computer.
Question 3.
What is a bit?
Answer:
A bit is the short form of Binary digit which can be ‘0’ or ‘1’. It is the basic unit of data in computers.
![]()
Question 4.
What is Decimal Number System?
Answer:
It consists of 0,1,2,3,4,5,6,7,8,9 (10 digits). It is the oldest and most popular number system used in our day-to-day life. In the positional number system, each decimal digit is weighted relative to its position in the number. This means that each digit in the number is multiplied by 10 raised to a power corresponding to that digit’s position.
Question 5.
What is meant by Octal Number System?
Answer:
Octal number system uses digits 0, 1, 2, 3, 4, 5, 6 and 7 (8 digits). Each octal digit has its own positional value or weight as a power of 8.
![]()
Question 6.
Convert (547)8 to its decimal equivalent?
Answer:
The Octal sequence (547)g has the decimal equivalent:
(547)8 = 5 × 82 + 4 × 81 + 7 × 80
= 5 × 64 + 4 × 8 + 7 × 1
= 320 + 32 + 7 – (359)10
Question 7.
Convert (65)10 into its equivalent binary number?
Answer:
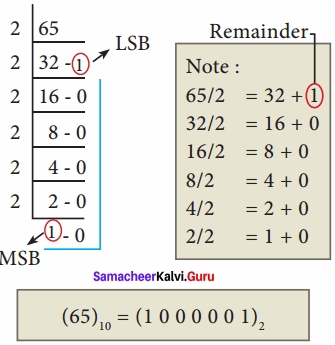
Question 8.
How will you convert decimal to octal? Give example?
Answer:
To convert Decimal to Octal, “Repeated Division by 8” method can be used. In this method, we have to divide the given number by 8.
Eg: Convert (65)10 into its equivalent Octal Number.
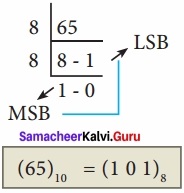
![]()
Question 9.
Write octal numbers and their binary equivalent?
Answer:
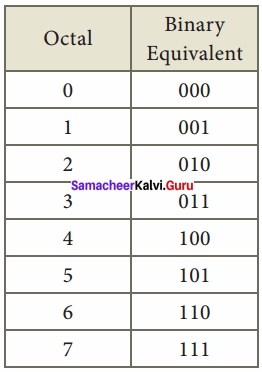
Question 10.
Convert (11010110)2 into octal equivalent?
Answer:
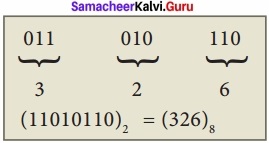
Question 11.
Convert the following binary numbers to decimal
(i) 11101
(ii) 1011010
Answer:

(11101)2 = (29)10
(ii) 1011010
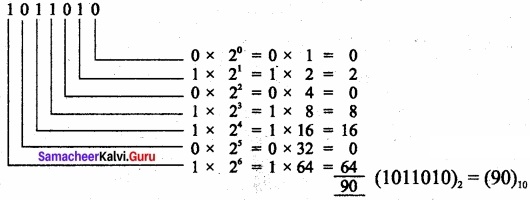
(1011010)2 = (90)10
Question 12.
Convert (3EF)16 to decimal?
Answer:

(3EF)16 = (1007)10
Question 13.
Convert (111011)2 into its equivalent decimal number?
Answer:
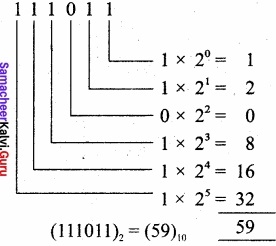
(111011)2 = (59)10
![]()
Question 14.
In what ways the numbers are represented in computers?
Answer:
The numbers are represented in computers in different ways:
- Signed Magnitude representation.
- 1 ’s Complement.
- 2’s Complement
Question 15.
What is a character set?
Answer:
In general, 26 uppercase letters, 26 lowercase letters, 0 to 9 digits and special characters are used in a computer is called character set. All these character set are denoted through numbers only.
III. Explain in Brief
Question 1.
Write the hierarchy of data representation?
Answer:
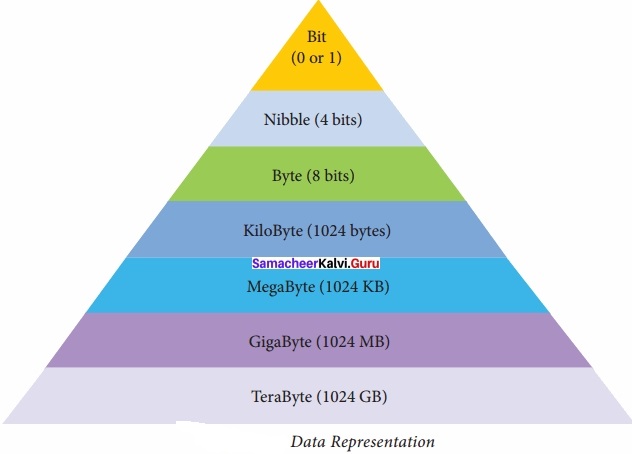
Question 2.
Write short note on hexadecimal number system?
Answer:
A hexadecimal number is represented using base 16. Hexadecimal or Hex numbers are used as a shorthand form of binary sequence. This system is used to represent data in a more compact manner. Since 16 symbols are used, 0 to F, the notation is called hexadecimal. The first 10 symbols are the same as in the decimal system, 0 to 9 and the remaining 6 symbols are taken from the first 6 letters of the alphabet sequence, A to F, where A represents 10, B is 11, C is 12, D is 13, E is 14 and F is 15.
Eg: The hexadecimal sequence (25)16 has the decimal equivalent:
(25)16 = 2 × 161 + 5 × 160
= 32 + 5 = (37)10
![]()
Question 3.
Write the steps for binary to decimal conversion?
Answer:
To convert Binary to Decimal we can use positional notation method.
- Step 1: Write down the Binary digits and list the powers of 2 from right to left (Positional Notation)
- Step 2: For each positional notation written for the digit, now write the equivalent weight.
- Step 3: Multiply each digit with its corresponding weight.
- Step 4: Add all the values.
Question 4.
How will you convert binary to octal?
Answer:
- Step 1: Group the given binary number into 3 bits from right to left.
- Step 2: You can add preceding 0 to make a group of 3 bits if the left most group has less than 3 bits.
- Step 3: Convert equivalent octal value using “2’s power positional weight method”.
Eg: Convert (11010110)2 to its Octal equivalent.
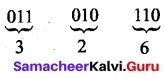
(11010110)2 = (326)8
![]()
Question 5.
Write the steps for converting binary to hexadecimal?
Answer:
- Step 1: Group the given number into 4 bits from right to left.
- Step 2: You can add preceding 0’s to make a group of 4 bits if the left most group has less than 4 bits.
- Step 3: Convert equivalent Hexadecimal value using “2’s power positional weight method”.
Eg: Convert (1111010110)2 to Hexadecimal.
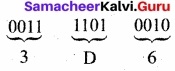
[Note: 0’s are added to the left most group to make it a group of 4 bits]
(1111010110)2 = (3D6)16
Question 6.
Write the steps for octal to decimal conversion?
Answer:
To convert octal to decimal, we can use positional notation method.
- Write down the octal digits and list the powers of 8 from right to left(Positional Notation).
- For each positional notation of the digit write the equivalent weight.
- Multiply each digit with its corresponding weight
- Add all the values
Eg: Convert (1265)8 to equivalent Decimal number.
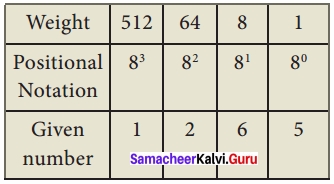
(1265)8 = 512 × 1 + 64 × 2 + 8 × 6 + 1 × 5
= 512 + 128 + 48 + 5
(1265)8 = (693)10
![]()
Question 7.
Write the steps for converting hexadecimal to decimal?
Answer:
To convert Hexadecimal to Decimal we can use positional notation method.
- Write down the Hexadecimal digits and list the powers of 16 from right to left (Positional Notation).
- For each positional notation written for the digit, now write the equivalent weight.
- Multiply each digit with its corresponding weight.
- Add all the values to get one final value.
Eg: Convert (25F)16 into its equivalent Decimal number.
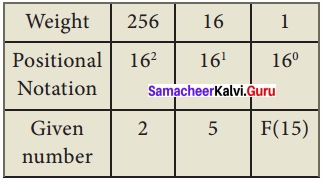
(25F)16 = 2 × 256 + 5 × 16 + 15 × 1
= 512 + 80 + 15
(25F)16 = (607)10
![]()
Question 8.
Write short note on signed magnitude representation?
Answer:
The value of the whole numbers can be determined by the sign used before it. If the number has ‘+’ sign or no sign it will be considered as positive. If the number has ‘-‘ sign it will be considered as negative.
Eg: + 43 or 43 is a positive number,
– 43 is a negative number.
In signed binary representation, the left most bit is considered as sign bit. If this bit is 0, it is a positive number and if it 1, it is a negative number. Therefore a signed binary number has 8 bits, only 7 bits used for storing values (magnitude) and the 1 bit is used for sign.
+ 43 is represented in memory as follows:

– 43 can be represented in memory as follows:

Question 9.
Write 2’s complement procedure with example?
Answer:
The 2’s-complement method for negative number is as follows:
- Invert all the bits in the binary sequence (i.e., change every 0 tol and every 1 to 0 i.e., 1’s complement)
- Add 1 to the result to the Least Significant Bit (LSB).
Eg: 2’s Complement represent of (-24)10

Question 10.
Write short note Unicode?
Answer:
This coding system is, used in most of the modem computers. The popular coding scheme after ASCII is Unicode. ASCII can represent only 256 characters. Therefore English and European Languages alone can be handled by ASCII. Particularly there was a situation, when the languages like Tamil, Malayalam, Kannada and Telugu could not be represented by ASCII. Hence, the Unicode was generated to handle all the coding system of Universal languages. This is 16 bit code and can handle 65536 characters.
IV. Explain in detail
Question 1.
Give the steps to convert fractional binary to decimal equivalent with example?
Answer:
Step 1: Convert integral part of Binary to Decimal equivalent using positional notation method.
Step 2: To convert the fractional part of binary to its decimal equivalent.
Step 2.1: Write down the Binary digits in the fractional part.
Step 2.2: For all the digits write powers of 2 from left to right starting from 2-1,2-22, 2-3………………… 2-n, now write the equivalent weight.
Step 2.3: Multiply each digit with its corresponding weight.
Step 2.4: Add all the values which you obtained in Step 2.3.
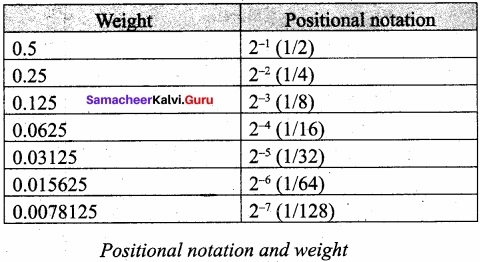
Step 3: To get final answer write the integral part (after conversion), followed by a decimal point(.) and the answer arrived at Step 2.4.
Eg: Convert the given Binary number (11.011)2 into its decimal equivalent Integer part (11)2 = 3.
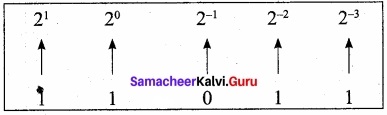
3 + (0 × 0.5 + 1 × 0.25 + 1 × 0.125) = 3. 375
(11.011)2 = (3.375)10
![]()
Question 2.
Explain in detail the different encoding systems used for computer?
Answer:
There are several encoding systems used for computer. They are –
(i) Binary Coded Decimal (BCD):
This encoding system is not in the practice right now. This is 26 bit encoding system. This can handle 26 = 64 characters only.
(ii) American Standard Code for Information Interchange (ASCII):
This is the most popular encoding system recognized by United States. Most of the computers use this system. Remember this encoding system can handle English characters only. This can handle 27 bit which means 128 characters.
In this system, each character has individual number. The new edition (version) ASCII – 8, has 28 bits and can handle 256 characters are represented from 0 to 255 unique numbers.
The ASCII code equivalent to the uppercase letter ‘ A’ is 65. The binary representation of ASCII (7 bit) value is 1000001. Also 01000001 in ASCII-8 bit.
(iii) Extended Binary Coded Decimal Interchange Code (EBCDIC):
This is similar to ASCII Code with 8 bit representation. This coding system is formulated by International Business Machine(IBM). The coding system can handle 256 characters. The input code in ASCII can be converted to EBCDIC system and vice – versa.
(iv) Indian Standard Code for Information Interchange (ISCII):
ISCII is the system of handling the character of Indian local languages. This as a 8-bit coding system. Therefore it can handle 256 (28) characters. This system is formulated by the department of Electronics in India in the year 1986-88 and recognized by Bureau of Indian Standards (BIS). Now this coding system is integrated with Unicode.
(v) Unicode:
This coding system is used in most of the modem computers. The popular coding scheme after ASCII is Unicode. ASCII can represent only 256 characters. Therefore English and European Languages alone can be handled by ASCII. Particularly there was a situation, when the languages like Tamil, Malayalam, Kannada and Telugu could not be represented by ASCII. Hence, the Unicode was generated to handle all the coding system of Universal languages. This is 16 bit code and can handle 65536 characters.