Samacheer Kalvi 10th Maths Guide Chapter 4 வடிவியல் Ex 4.1

Tamilnadu State Board New Syllabus Samacheer Kalvi 10th Maths Guide Pdf Chapter 4 வடிவியல் Ex 4.1 Textbook Questions and Answers, Notes.

TN Board 10th Maths Solutions Chapter 4 வடிவியல் Ex 4.1

கேள்வி 1.
கீழே கொடுக்கப்பட்டவற்றில் எந்த முக்கோணங்கள் வடிவொத்தவை என்பதைச் சோதிக்கவும். மேலும் X-யின் மதிப்பு காண்க.


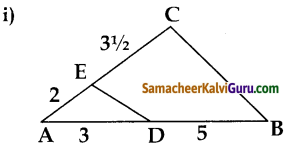
தீர்வு :
i) ΔAED, ΔACB ல்

∴ ΔAED ஆனது ΔACD – க்கு வடிவொத்தவை அல்ல

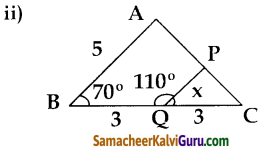
ii) ΔABC, ΔPQC இவற்றில்
∠A, ∠C பொது
∴ AA விதிமுறைப்படி
ΔABC ~ ΔPQC
மற்றும் ∠B = ∠PQC = 70°
∴ AB ஆனது PQ க்கு இணை
∴ PQ = \(\frac{\mathrm{AB}}{2}=\frac{5}{2}\)
x = 2.5

கேள்வி 2.
ஒரு பெண் விளக்கு கம்பத்தின் அடியிலிருந்து 6.6 மீ தொலைவிலுள்ள கண்ணாடியில் விளக்கு கம்பத்தின் உச்சியின் பிரதிலிப்பைக் காண்கிறாள். 1.25 மீ உயரமுள்ள அப்பெண் கண்ணாடியிலிருந்து 2.5 மீ தொலைவில் நிற்கிறாள். கண்ணாடியானது வானத்தை நோக்கி வைக்கப்பட்டுள்ளது. அப்பெண், கண்ணாடி மற்றும் விளக்கு கம்பம் ஆகியவை எல்லாம் ஒரே நேர்க்கோட்டில் அமைவதாக எடுத்துக் கொண்டால், விளக்குக் கம்பத்தின் உயரத்தைக் காண்க.
தீர்வு :

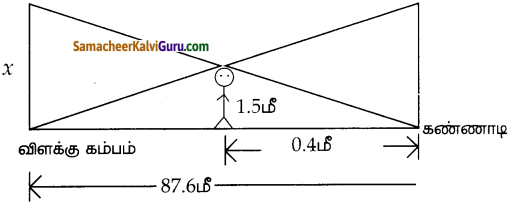
படத்திலிருந்து, \(\frac{x}{1.5}=\frac{87.6}{0.4}\)
⇒ x = \(\frac{87.6}{0.4}\) x 1.5
= 328.5 மீ

கேள்வி 3.
6 மீ உயரமுள்ள செங்குத்தாக நிற்கும் கம்பமானது தரையில் 400 செ.மீ நீளமுள்ள நிழலை ஏற்படுத்துகிறது. ஒரு கோபுரமானது 28மீ நீளமுள்ள நிழலை ஏற்படுத்துகிறது. கம்பம் மற்றும் கோபுரம் ஒரே நேர்கோட்டில் அமைவதாகக் கருதி வடிவொத்த தன்மையைப் பயன்படுத்தி, கோபுரத்தின் உயரம் காண்க.
தீர்வு :

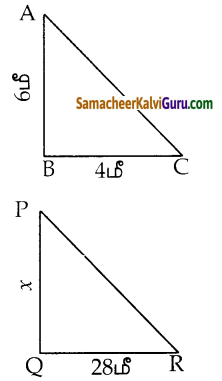
படத்தில் ∠ABC = ∠PQR = 90°
∠ACB = ∠PRQ
ΔBCA ~ ΔQRP
∴ \(\frac{\mathrm{AB}}{\mathrm{PQ}}=\frac{\mathrm{BC}}{\mathrm{QR}}\)
\(\frac{6}{x}=\frac{4}{28}\)
⇒ 4x = 6 x 28
x = \(\frac{6 \times 28}{4}\)
= 42மீ

கேள்வி 4.
QR ஐ அடிபக்கமாகக் கொண்ட இரு முக்கோணங்கள் QPR மற்றும் QSRயின் புள்ளிகள் P மற்றும் S யில் செங்கோணங்களாக அமைந்துள்ளன. இரு முக்கோணங்களும் QR யின் ஒரே பக்கத்தில் அமைந்துள்ளன. PR மற்றும் SQ என்ற பக்கங்கள் T என்ற புள்ளியில் சந்திக்கின்றன எனில், PT X TR = ST x TQ என நிறுவுக.
தீர்வு :

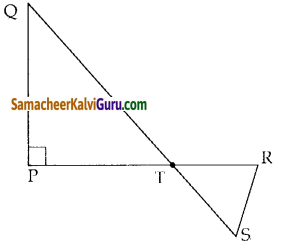
ΔPQT, ΔTSR இவற்றில்
∠P = ∠S = 90° மற்றும்
∠PTO = ∠STR (குத்தெதிர் கோணங்கள்)
∴ AA விதிமுறைப்படி
ΔPQT ~ ΔTSR
∴ \(\frac{\mathrm{QT}}{\mathrm{TR}}=\frac{\mathrm{PT}}{\mathrm{TS}}\)
⇒ QT × TS = PT × TR

கேள்வி 5.
கொடுக்கப்பட்ட படத்தில், C ஐ செங்கோணமாகக் கொண்ட Δ ABC யில் DE ⊥ AB எனில் ΔABC ~ ΔADE என நிரூபிக்க . மேலும் AE மற்றும் DE ஆகியவற்றின் நீளங்களைக் காண்க.
தீர்வு :
∠A பொது
∠AED = ∠BCA = 90°

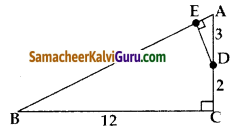
∴ AA விதிமுறைப்படி
ΔABC ~ ΔADE மற்றும்
AB² = AC² + BC²
= 5² + 12²
= 25 + 144 = 169°
AB = 13
ΔABC ~ΔADE

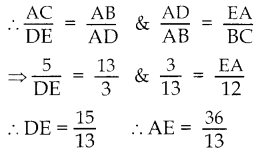
கேள்வி 6.
கொடுக்கப்பட்ட படத்தில், ΔACB ~ ΔAPQ. BC = 8 செ.மீ, PQ = 4 செ.மீ, BA = 6.5 செ.மீ மற்றும் AP = 2.8 செ.மீ எனில் CA மற்றும் AQ யின் மதிப்பைக் காண்க.

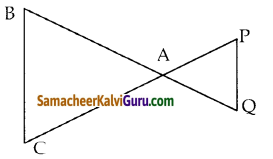
தீர்வு :
ΔACB ~ ΔAPQ
\(\frac{\mathrm{BC}}{\mathrm{PQ}}=\frac{\mathrm{CA}}{\mathrm{AP}}\)
\(\frac{8}{4}=\frac{C A}{2.8}\)
= CA = \(\frac { 8 }{ 4 }\) x 2.8
= 5.6 செ.மீ
மற்றும் \(\frac{B C}{P Q}=\frac{B A}{A Q}\)
⇒ \(\frac{8}{4}=\frac{6.5}{\mathrm{AQ}}\)
⇒ AQ = 6.5 x \(\frac{4}{8}\)
= 3.25 செ.மீ

கேள்வி 7.
கொடுக்கப்பட்ட படத்தில் OPQR ஆனது சதுரம் மற்றும் ∠MLN = 90° எனில், கீழ்க்கண்டவற்றை நிரூபிக்கவும். i) ΔLOP ~ ΔQMO
ii) ΔLOP ~ ΔRPN
iii) ΔQMO ~ ΔRPN
iv) QR² = MQ x RN

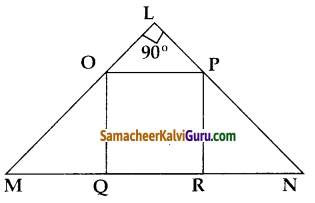
தீர்வு : i) ΔLOP, ΔQMO இவற்றில்

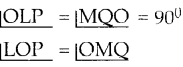
[ ∵ ஒத்த கோணங்கள் சமம்]
∴ ΔLOP ~ ΔQMO

ii) ΔLOP, ΔRPN இவற்றில்

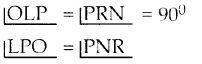
[ ∵ ஒத்த கோணங்கள் சமம்]
∴ ΔLOP ~ ΔRPN

iii) (i) & (ii) லிருந்து
ΔLOP ~ ΔQMO & ΔLOP ~ ΔRPN
∴ ΔQMO ~ ΔRPN

iv) ΔQMO ~ ΔRPN
QO × RP = MQ × RN
⇒ QR² = MQ x RN [∵ OPQR சதுரம்]

கேள்வி 8.
ΔABC ~ ΔDEF – ல் , Δ ABC யின் பரப்பு 9 செ.மீ² ΔDEF யின் பரப்பு 16 செ.மீ 2 மற்றும் BC=2.1 செ.மீ எனில், EFயின் நீளம் காண்க.
தீர்வு :
கணக்கின் படி ΔABC ~ ΔDEF
இரு வடிவொத்த முக்கோணங்களின் பரப்பளவுகளின் விகிதம் அவற்றின் ஒத்த பக்கங்களின் வர்க்கங்களின் விகிதத்திற்குச் சமம்.

= 9 × EF² = 16 × (2.1)²
∴ EF² = \(\frac{16 \times(2.1)^{2}}{9}\)
= 7.84
∴ EF = 2.8 செ.மீ

கேள்வி 9.
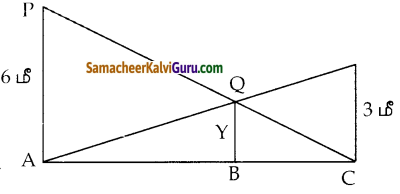
6மீ மற்றும் 3மீ உயரமுள்ள இரண்டு செங்குத்தான தூண்கள் AC என்ற தரையின் மேல் படத்தில் காட்டியுள்ளவாறு ஊன்றப்பட்டுள்ளது எனில் , y யின் மதிப்பு காண்க.
தீர்வு :
WKT தூண்களின் உச்சியிலிருந்து எதிரேயுள்ள தூண்களின் அடிக்கு வரையப்படும் கோடுகள் சந்திக்கும் புள்ளியின் உயரமானது \(\frac{a b}{a+b}\) மீ ஆகும்.
∴ y = \(\frac{6 \times 3}{6+3}\)
= \(\frac{18}{9}\) = 2மீ

கேள்வி 10.
கொடுக்கப்பட்ட முக்கோணம் POR – யின் ஒத்த பக்கங்களின் விகிதம் \(\frac { 2 }{ 3 }\) அமையுமாறு ஒரு வடிவொத்த முக்கோணம் வரைக. (அளவு காரணி \(\frac { 2 }{ 3 }\) < 1).
தீர்வு :

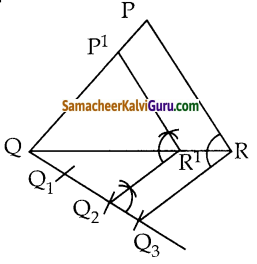
வரைமுறை :

1. ஏதேனும் ஒரு அளவைக் கொண்டு ΔPQR வரைக.
2. QR என்ற கோட்டுத் துண்டில் குறுங்கோணத்தை ஏற்படுத்துமாறு, QX என்ற கதிரை P என்ற முனைப்புள்ளிக்கு எதிர்திசையில் வரைக.
3. QX ன் மீது Q₁, Q₂, Q₃ என்ற மூன்று புள்ளிகளை QQ₁ = Q₁Q₂ = Q₂Q₃ என்றவாறு குறிக்கவும்.
4. Q₃R ஐ இணைத்து Q₂, யிலிருந்து Q₃R க்கு இணையாக ஒரு கோடு வரைக. இது QR ஐ R’ல் சந்திக்கிறது.
5. R’ லிருந்து RP க்கு இணையாக வரையப்படும் கோடு QP ஐ P’ ல் சந்திக்கிறது. ΔP’QR’ ன் பக்கங்கள் ΔPQRன் ஒத்த பக்கங்களின் அளவில் \(\frac { 2 }{ 3 }\) ஆகும்.
6. ΔP’QR’ ஆனது தேவையான வடிவவொத்த முக்கோணம் ஆகும்.

கேள்வி 11.
கொடுக்கப்பட்ட முக்கோணம் LMN ன் ஒத்த பக்கங்களின் விகிதம் \(\frac { 4 }{ 5 }\) என அமையுமாறு ஒரு வடிவொத்த முக்கோணம் வரையக.(அளவு காரணி \(\frac { 4 }{ 5 }\) < 1).
தீர்வு :

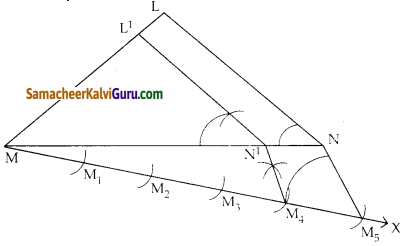
வரைமுறை :

1. ஏதேனும் ஓர் அளவைக் கொண்டு ΔLMN வரைக.
2. MN என்ற கோட்டுத் துண்டில் குறுங்கோணத்தை ஏற்படுத்துமாறு, MX என்ற கதிரை L என்ற முனைப்புள்ளிக்கு எதிர் திசையில் வரைக.
3. MX – யின் மீது M₁, M₂, M₃, M₄, M₅; என்ற 5 புள்ளிகளை MM₁ = M₁M₂ = M₂M₃ = M₄M₅ என்றவாறு குறிக்க.
4. M₅N – ஐ இணைத்து M, லிருந்து M₅N க்கு இணையாக ஒரு கோடு வரைக. இது MN – ஐ N’ல் சந்திக்கும்.
5. N’ லிருந்து NL க்கு இணையாக வரையப்படும் கோடு LM ஐ L’ல் சந்திக்கும். ΔL’MN’ ன் பக்கங்கள் ΔLMN ன் ஒத்த பக்கங்களின் அளவில் 5 ல் 4 பங்கு ஆகும்.
6. ΔL’MN’ ஆனது தேவையான வடிவொத்த முக்கோணம் ஆகும்.

கேள்வி 12.
கொடுக்கப்பட்ட முக்கோணம் ABC யின் ஒத்த பக்கங்களின் விகிதம் \(\frac { 6 }{ 5 }\) என அமையுமாறு ஒரு வடிவொத்த முக்கோணம் வரைக. (அளவு காரணி \(\frac { 6 }{ 5 }\) > 1).

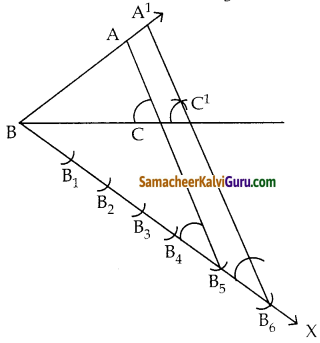
வரைமுறை :

1. ஏதேனும் ஓர் அளவைக் கொண்டு ΔABC வரைக
2. BC என்ற கோட்டுத்துண்டில் குறுங்கோணத்தை ஏற்படுத்துமாறு BX என்ற கதிரை A என்ற முனைப்புள்ளிக்கு எதிர் திசையில் வரைக.
3. BX – ன் மீது B₁, B₂, B₃, B₄, B₅, B₆, என்ற 6 புள்ளிகளை BB₁ = B₁B₂ = B₂B₃ = B₄B₅ = B₅B₆
   என்றவாறு குறிக்க.
4. B₅ ஐ புள்ளி ( வுடன் இணைக்க . B₅C க்கு இணையாக B₆ லிருந்து = வரையப்படும் கோடு BC ஐ C’ ல் சந்திக்கிறது.
5. ΔA’BC’ ஆனது தேவையான வடிவொத்த முக்கோணம் ஆகும்.

கேள்வி 13.
கொடுக்கப்பட்ட முக்கோணம் PQR ன் ஒத்த பக்கங்களின் விகிதம் \(\frac { 7 }{ 3 }\) என்றவாறு ஒரு வடிவொத்த முக்கோணம் வரைக. (அளவு காரணி \(\frac { 7 }{ 3 }\) > 1)
தீர்வு :

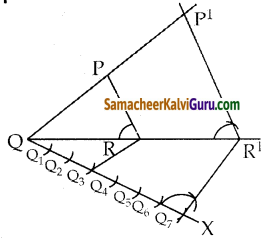
வரைமுறை :

1. ஏதேனும் ஓர் அளவைக்கொண்டு ΔPQR வரைக.
2. QR – ல் குறுங்கோணத்தை ஏற்படுத்துமாறு QX
3. QX ன் மீது Q₁, Q₂, Q₃, Q₄, Q₅, Q₆, Q₇ ஐ குறிக்க
4. Q₃R ஐ இணை Q₃R R’க்கு இணையாக Q₇ – லிருந்து வரையப்படும் கோடு QR ஐ R-ல் சந்திக்கும்.
5. Rலிருந்து PR க்கு இணையாக வரையப்படும் கோடு PQ ஐ P’ல் சந்திக்கும்.
6. ΔP’QR’ ன்பக்கங்கள் ΔPQR ன் ஒத்த பக்கங்களின் அளவில் \(\frac { 7 }{ 3 }\) பங்கு
7. ΔP’QR’ தேவையான முக்கோணம் ஆகும்.

அடிப்படை விகிதச்சம் தேற்றம் (or) தேல்ஸ் தேற்றம்
கூற்று: ஒரு நேர்க்கோடு முக்கோணத்தின் ஒரு பக்கத்திற்கு இணையாகவும் மற்ற இரு பக்கங்களை வெட்டுமாறும் வரையப்பட்டால் அக்கோடு அவ்விரண்டு பக்கங்களையும் சம விகிதத்தில் பிரிக்கும்.
நிரூபணம் :

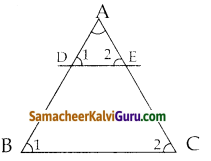
கொடுக்கப்பட்டவை : ΔABCல், AB ன் மீது D ம், ACன் மீது E ம் உள்ளது.
அமைப்பு : DE|| BC வரைக
நிரூபிக்க : \(\frac{A D}{D B}=\frac{A E}{E C}\)

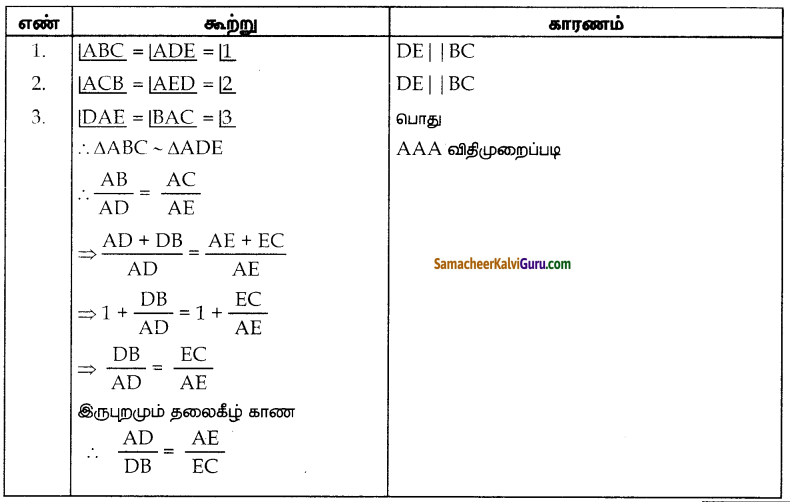
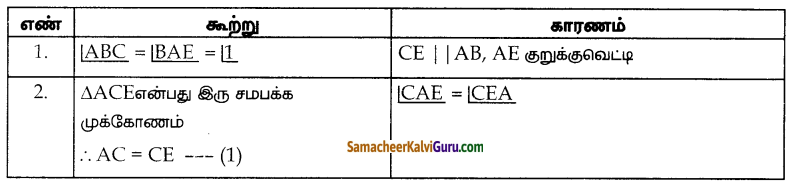
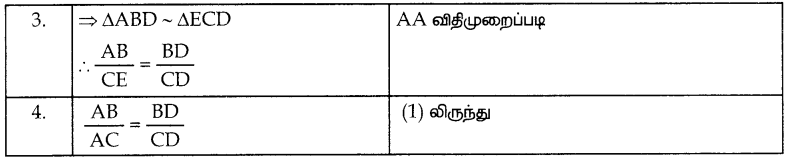
கோண இருசமவெட்டி தேற்றம்

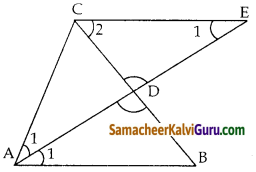
கூற்று :
ஒரு முக்கோணத்தின் ஒரு கோணத்தின் உட்புற இருசம வெட்டியானது அக்கோணத்தின் எதிர்பக்கத்தை உட்புறமாக அக்கோணத்தினை அடக்கிய பக்கங்களின் விகிதத்தில் பிரிக்கும்.
கொடுக்கப்பட்டவை : ΔABC ல், AD என்பது ∠A ன் உட்புற இருசமவெட்டி
நிரூபிக்க : \(\frac{A B}{A C}=\frac{B D}{C D}\)
அமைப்பு : AB க்கு இணையாக C வழியாக CE வரைக்