You can Download Samacheer Kalvi 10th Maths Book Solutions Guide Pdf, Tamilnadu State Board help you to revise the complete Syllabus and score more marks in your examinations.
Tamilnadu Samacheer Kalvi 10th Maths Solutions Chapter 6 Trigonometry Ex 6.1
10th Maths Exercise 6.1 Samacheer Kalvi Question 1.
Prove the following identities.
(i) cot θ + tan θ = sec θ cosec θ
(ii) tan4θ + tan2θ = sec4θ – sec2θ
Solution:

10th Maths Trigonometry Exercise 6.1 Question 2.
Prove the following identities
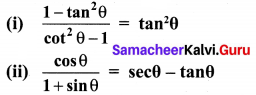
Solution:


Exercise 6.1 Class 10 Samacheer Kalvi Question 3.
Prove the following identities

Solution:


10th Trigonometry Exercise 6.1 Question 4.
Prove the following identities
(i) sec6θ = tan6θ + 3tan2θ sec2θ + 1
(ii) (sinθ + secθ)2 + (cosθ + cosecθ)2
= 1 + (secθ + cosecθ)2
(i) L.H.S = sec6θ = (sec2θ)3 = (1 + tan2θ )3 = (tan2θ + 1)3
(a + b)3 = a3 + 3a2b + 3ab2 + b3
= (tan2θ)3 + 3(tan2θ)2 × 1 + 3 × tan2θ × 12 + 1
= tan6θ + 3tan2θ × (sec2θ – 1) + 3tan2θ + 1
= tan6θ + 3tan2θsec2θ – 3tan2θ + 3tan2θ +1
= tan6θ + 3tan2θ sec2θ + 1 = R.H.S
(ii) L.H.S = (sinθ + secθ )2 + (cosθ + cosecθ)2
= sin2θ + 2sinθ secθ + sec2θ + cos2θ + 2cosθ cosecθ+ cosec2θ
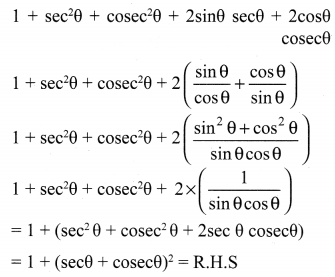
Ex 6.1 Class 10 Samacheer Question 5.
Prove the following identities
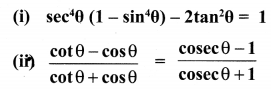
Solution:
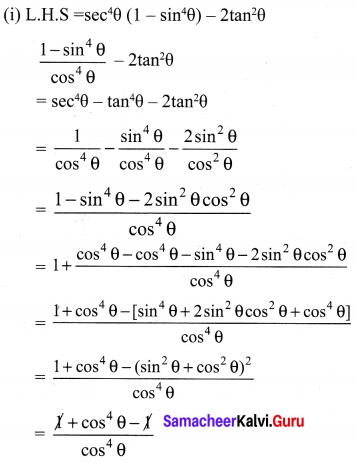
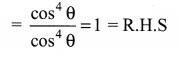
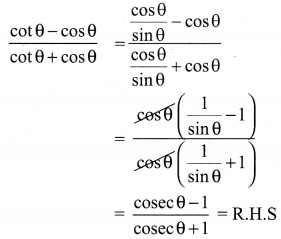
10th Maths Exercise 6.1 Question 6.
Prove the following identities
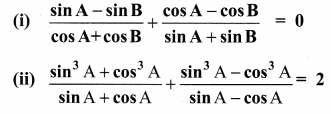
Solution:

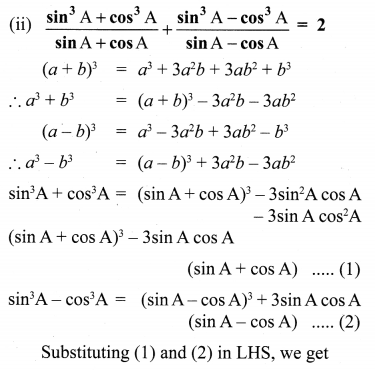
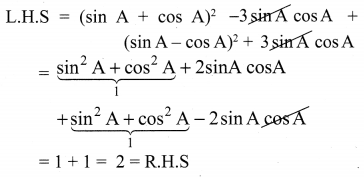
Trigonometry Exercise 6.1 Question 7.
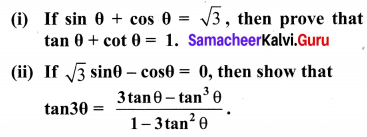
Solution:


10th Maths 6.1 Question 8.
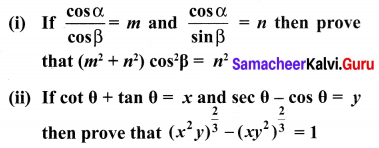
Solution:
(i) LHS:

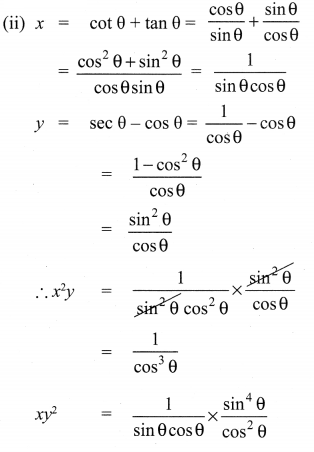
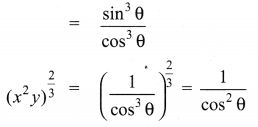
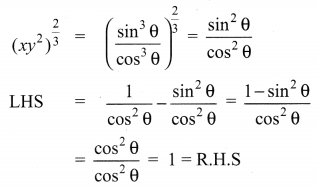
10th Maths Exercise 6.1 In Tamil Question 9.
(i) If sinθ + cosθ = p and secθ + cosecθ = q then prove that q(p2 – 1) = 2p
(ii) If sinθ(1 + sin2θ) = cos2θ, then prove that cos6θ – 4cos4θ + 8cos2θ = 4
Solution:

(ii) Given sinθ(1 + sin2θ) = cos2θ
Sustitute sin2θ = 1 – co2θ and take cos θ = c
squaring (1) on bothsides we get
sin2θ(1 + sin2θ)2 = cos4θ
(1 – c2)(1 + 1 – c2) = c4
(1 – c2)(2 – c2)2 = c4
(1 – c2)(4 + c4– 4c2) = c4
4 + c4– 4c2 – 4c2 – c6 + 4c4 = c4
-c6 + 4c4 – 8c2 = -4
c6 – 4c4 + 8c2 = -4
ie cos 6θ – 4cos 4θ + 8cos2θ = 4 = RHS
∴ Hence proved
10th Samacheer Kalvi Maths Trigonometry Question 10.

Solution:
