You can Download Samacheer Kalvi 10th Maths Book Solutions Guide Pdf, Tamilnadu State Board help you to revise the complete Syllabus and score more marks in your examinations.
Tamilnadu Samacheer Kalvi 10th Maths Solutions Chapter 6 Trigonometry Additional Questions
Question 1.
Given tan A = \(\frac{4}{3}\), find the other trigonometric ratios of the angle A.
Solution:
Let us first draw a right ∆ABC.
Now, we know that tan A = \(\frac{\mathrm{BC}}{\mathrm{AB}}=\frac{4}{3}\)
Therefore, if BC = 4k, then AB = 3k, where k is a positive number.
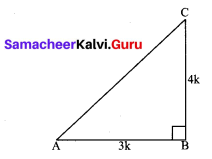
Now, by using the pythagoras theorem, we have
AC2 = AB2 + BC2
= (4k)2 + (3k)2 = 25 k2
AC = 5k
So,
Now, we can write all the trigonometric ratios using their definitions.

Question 2.
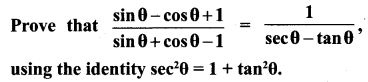
Solution:
Since we will apply the identity involving sec θ and tan θ, let us first convert the LHS (of the identity we need to prove) in terms of sec θ and tan θ by dividing numerator and denominator by cos θ.

Which is the RHS of the identity, we are required to prove.
![]()
Question 3.
Prove that sec A (1 – sin A) (sec A + tan A) = 1.
Solution:
LHS = sec A(1 – sin A)(sec A + tan A)
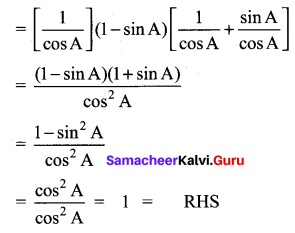
Question 4.
In a right triangle ABC, right-angled at B, if tan A = 1, then verify that 2 sin A cos A = 1.
Solution:
In ABC, tan A = \(\frac{B C}{A B}\)
Let AB = BC = k, where k is a positive number.
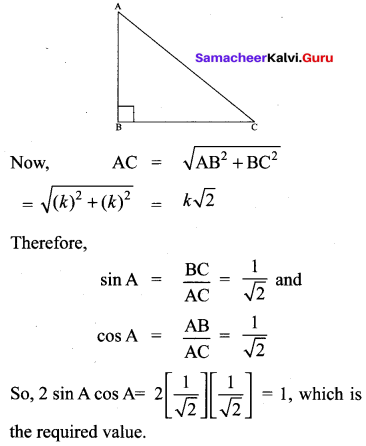
![]()
Question 5.
If sin (A – B) = \(\frac{1}{2}\), cos (A + B) = \(\frac{1}{2}\), 0° < A + B ≤ 90°, A > B, find A and BC
Solution:

We get,
A = 45° and B = 15°
Question 6.
Express the ratios cos A, tan A and sec A in terms of sin A.
Solution:
Since
cos2A + sin2A = 1, therefore,
cos2A = 1 – sin2A
i.e., cos A = \(\pm \sqrt{1-\sin ^{2} A}\)
This gives cos A = \(\sqrt{1-\sin ^{2} A}\)
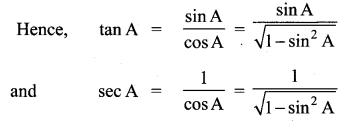
Question 7.
Evaluate \(\frac{\tan 65^{\circ}}{\cot 25^{\circ}}\)
Solution:
We know:
cot A = tan(90° – A)
So,

![]()
Question 8.
Since sin 3A = cos(A – 26°), where 3A is an acute angle, find the value at A.
Solution:
We are given that sin 3A = cos (A – 26°) ….. (1)
Since sin 3A = cos(90° – 3A) we can write (1) as cos(90° – 3A) = cos(A – 26°)
Since 90° – 3A and A – 26° are both acute angles.
90° – 3A = A – 26°
which gives A = 29°
Question 9.
Express cot 85° + cos 75° in terms of trigonometric ratios of angles between 0° and 45°.
Solution:
cot 85° +cos 75°
= cot(90° – 5°) + cos(90° – 15°)
= tan 5° + sin 15°
![]()
Question 10.
From a point on a bridge across a river, the angles of depression of the banks on opposite sides at the river are 30° and 45°, respectively. If the bridge is at a height at 3 m from the banks, find the width at the river.
Solution:
A and B represent points on the bank on opposite sides at the river, so that AB is the width of the river. P is a point on the bridge at a height of 3m i.e., DP = 3 m. We are interested to determine the width at the river which is the length at the side AB of the ∆APB.
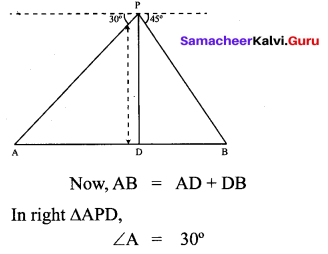

Also, in right ∆PBD,
B = 45°
So, BD = PD = 3 m
Now, AB = BD + AD
= 3 + \(3 \sqrt{3}\) = 3(1 + \(\sqrt{3}\))m
Therefore, the width at the river is 3(\(\sqrt{3}\) + 1)