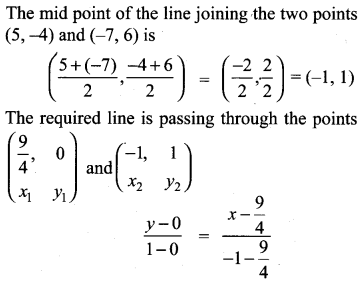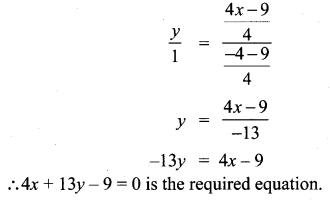You can Download Samacheer Kalvi 10th Maths Book Solutions Guide Pdf, Tamilnadu State Board help you to revise the complete Syllabus and score more marks in your examinations.
Tamilnadu Samacheer Kalvi 10th Maths Solutions Chapter 5 Coordinate Geometry Ex 5.4
10th Maths Exercise 5.4 Samacheer Kalvi Question 1.
Find the slope of the following straight lines
(i) 5y – 3 = 0
(ii) \(7 x-\frac{3}{17}\) = 0
Solution:

Exercise 5.4 Class 10 Samacheer Kalvi Question 2.
Find the slope of the line which is
(i) parallel to y = 0.7x -11
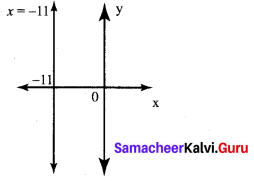
(ii) perpendicular to the line x = -11
Solution:
(i) y = 0.7x – 11
line parallel to y = 0.7x – 11 is y = 0.7x + C
If the lines are parallel, slopes are equal
∴ The slope of the required line is 0.7.
(ii) m = tan θ = tan 90°= ∞ undefined.
Ex 5.4 Class 10 Samacheer Question 3.
Check whether the given lines are parallel or perpendicular
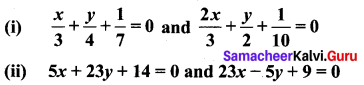
Solution:
(i) \(\frac{x}{3}+\frac{y}{4}+\frac{1}{7}\) = 0
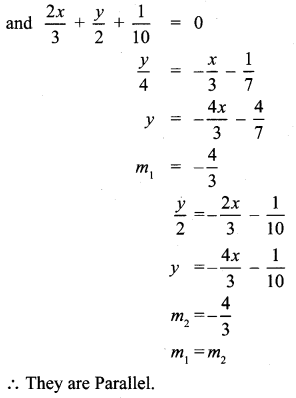
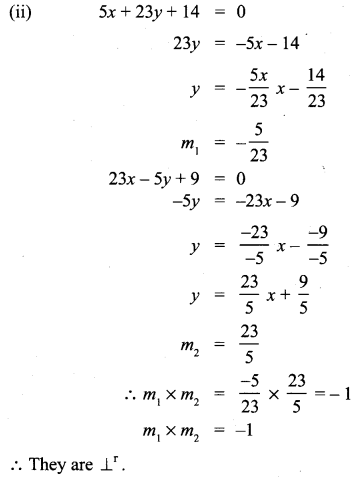
10th Maths Exercise 5.4 Question 4.
If the straight lines 12y = -(p + 3)x + 12, 12x – 7y = 16 are perpendicular then find ‘p’.
Solution:


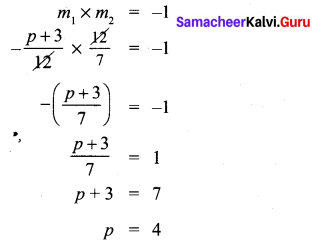
10th Maths Example 5.4 Question 5.
Find the equation of a straight line passing through the point P (-5, 2) and parallel to the line joining the points Q(3, -2) and R(-5, 4).
Solution:

Class 10 Maths Exercise 5.4 Solutions Question 6.
Find the equation of a line passing through ; (6, -2) and perpendicular to the line joining the points (6, 7) and (2, -3).
Solution:
Slope of line joining (6, 7) and (2,-3) is

5 Coordinate Geometry Question 7.
A(-3, 0) B(10, – 2) and C(12, 3) are the vertices of ∆ABC . Find the equation of the altitude through A and B.
Solution:
A(-3, 0), B(10, -2), C(12, 3)
Since AD ⊥ BC
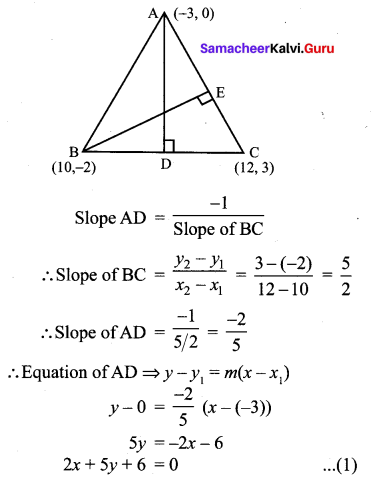
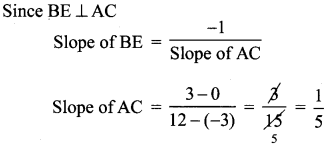
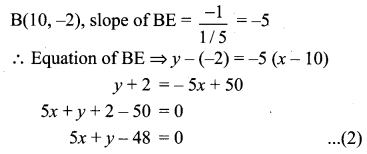
(1), (2) are the required equations of the altitudes through A and B.
5.4 Geometry Question 8.
Find the equation of the perpendicular bisector of the line joining the points A(-4, 2) and B(6, -4).
Solution:
Mid Point AB is
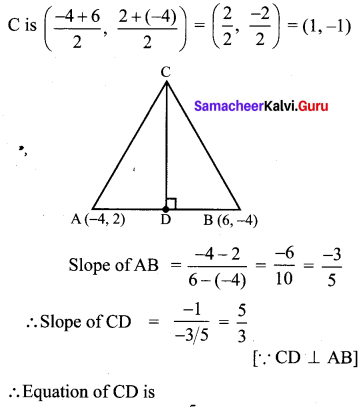
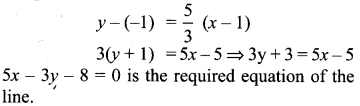
Ex 5.4 Class 10 Question 9.
Find the equation of a straight line through the intersection of lines 7x + 3y = 10, 5x – 4y = 1
and parallel to the line 13x + 5y + 12 = O
Solution:
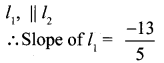
l1 passes through the intersecting point.

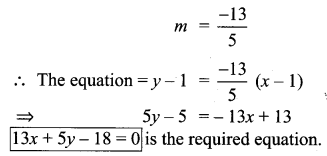
10th Samacheer Kalvi Maths Coordinate Geometry Question 10.
Find the equation of a straight line through the intersection of lines 5x – 6y = 2, 3x + 2y = 10 and perpendicular to the line 4x – 7y + 13 = 0
Solution:
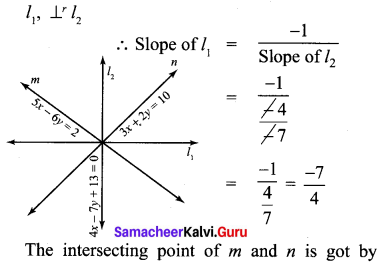


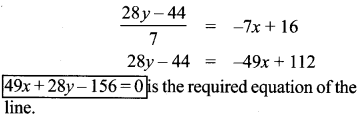
12th Maths Exercise 5.4 Samacheer Kalvi Question 11.
Find the equation of a straight line joining the point of intersection of 3x + y + 2 = 0 and x – 2y – 4 = 0 to the point of intersection of 7x – 3y = -12 and 2y = x + 3
Solution:

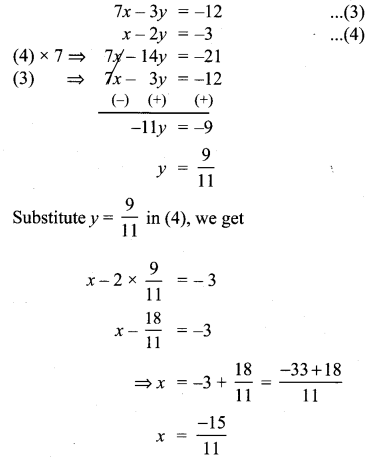

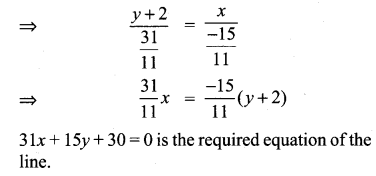
Exercise 5.4 Class 10 Question 12.
Find the equation of a straight line through the point of intersection of the lines 8x + 3+ = 18, 4x + 5+ = 9 and bisecting the line segment joining the points (5, -4) and (-7, 6).
Solution:
The intersecting point of the lines