Samacheer Kalvi 10th Maths Solutions Chapter 3 Algebra Ex 3.2

You can Download Samacheer Kalvi 10th Maths Book Solutions Guide Pdf, Tamilnadu State Board help you to revise the complete Syllabus and score more marks in your examinations.

Tamilnadu Samacheer Kalvi 10th Maths Solutions Chapter 3 Algebra Ex 3.2

10th Maths Exercise 3.2 Samacheer Kalvi Question 1.
Find the GCD of the given polynomials
(i) x⁴ + 3x³ – x – 3, x³ + x² – 5x + 3
(ii) x⁴ – 1, x³ – 11x² + x – 11
(iii) 3x⁴ + 6x³ – 12x⁴ – 24x, 4x⁴ + 14x³ + 8x² – 8x
(iv) 3x³ + 3x² + 3x + 3, 6x³ + 12x² + 6x + 12
Solution:
x⁴ + 3x³ – x – 3, x³ + x² – 5x + 3
Let f(x) = x⁴ + 3x³ – x – 3
g(x) = x³ + x² – 5x + 3

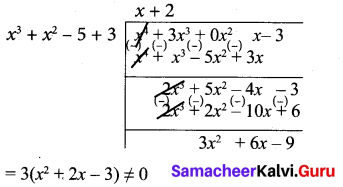
Note that 3 is not a divisor of g(x). Now dividing g(x) = x³ + x² – 5x + 3 by the new remainder x² + 2x – 3 (leaving the constant factor 3) we get

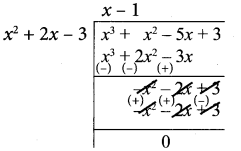
Here we get zero remainder
G.C.D of (x⁴ + 3x³ – x – 3), (x³ + x² – 5x + 3) is (x² + 2x – 3)

(ii) x⁴ – 1, x³ – 11x² + x – 11

(iii) 3x⁴ + 6x³ – 12x² – 24x, 4x⁴ + 14x³ + 8x² – 8x
4x⁴ + 14x³ + 8x² – 8x = 2 (2x⁴ + 7x³ + 4x² -4x)
Let us divide
(2x⁴ + 7x³ + 4x² + 4x) by x⁴ + 2x³ – 4x² – 8x

(x³ + 4x³ + 4x) ≠ 0
Now let us divide
x⁴ + 2x³ – 4x² – 8x by x³ + 4x² + 4x

∴ x³ + 4x² + 4x is the G.C.D of 3x⁴ + 6x³ -12x² – 24x, 4x⁴ + 14x³ + 8x² -8x
∴ Ans x (x² + 4x + 4)

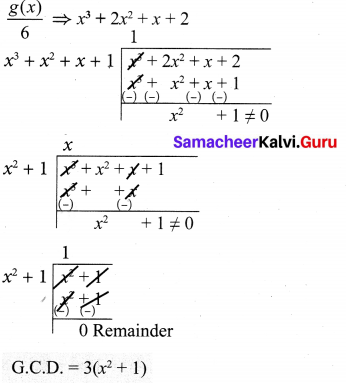
(iv) f(x) = 3x³ + 3x² + 3x + 3 = 3(x³ + x² + x + 1)
g(x) = 6x³ + 12x² + 6x + 12
= 6(x³ + 2x² + x + 2)
= 2 × 3 (x³ + 2x² + x + 2)
f(x) ⇒ x³ + x² + x + 1

Ex 3.2 Class 10 Samacheer Question 2.
Find the LCM of the given expressions,
(i) 4x²y, 8x³y²
(ii) -9a³b², 12a²b²c
(iii) 16m, -12m²n², 8n²
(iv) p² – 3p + 2, p² – 4
(v) 2x² – 5x – 3, 4x² – 36
(vi) (2x² – 3xy)², (4x – 6y)³, 8x³ – 27y³
Solution:
(i) 4x²y, 8x³y²
4x²y = 2 × 2 x²y
8x³y² = 2 × 2 × 2 x³y²
L.C.M. = 2 × 2 × 2 x³y²
= 8x³ y²

(ii) -9a³b² = -3 × 3 a³b²
12a²b²c = 2 × 3 × 2a²b²c
L.C.M. = -3 × 3 × 2 × 2 a³b²c
= -36a³b²c

(iii) 16m, -12m²n², 8n²
16 m = 2 × 2 × 2 × 2 × m
-12m²n² = -2 × 2 × 3 × m²n²
8n² = 2 × 2 × 2 × n²
L.C.M.= -2 × 2 × 2 × 2 × 3 m²n²
= -48 m²n²

(v) 2x² – 5x – 3, 4x² – 36
2x² – 5x – 3 = (x – 3)(2x + 1)
4x² – 36 = 4(x + 3)(x – 3)
L.C.M. = 4(x + 3)(x – 3)(2x + 1)

(vi) (2x² – 3xy)² = (x(2x – 3y))²
(4x – 6y)³ = (2(2x – 3y))³
8x³ – 27y³= (2x)³ – (3y)³
= (2x – 3y) (4x² + 6xy + 9y²)
L.C.M. = 2³ × x² (2x – 3y)³ (4x² + 6xy + 9y²)