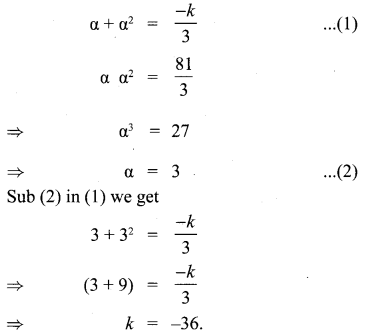Samacheer Kalvi 10th Maths Solutions Chapter 3 Algebra Ex 3.14

You can Download Samacheer Kalvi 10th Maths Book Solutions Guide Pdf, Tamilnadu State Board help you to revise the complete Syllabus and score more marks in your examinations.

Tamilnadu Samacheer Kalvi 10th Maths Solutions Chapter 3 Algebra Ex 3.14

Ex 3.14 Class 10 Samacheer Question 1.
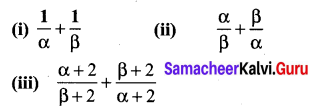
Write each of the following expression in terms of α + β and αβ.

Solution:

10th Maths Exercise 3.14 Samacheer Kalvi Question 2.
The roots of the equation 2x² – 7x + 5 = 0 are α and β. Without solving the root find

Solution:
2x² – 7x + 5 = x² – \(\frac{7}{2} x+\frac{5}{2}\) = 0
α + β = \(\frac{7}{2}\)
αβ = \(\frac{5}{2}\)

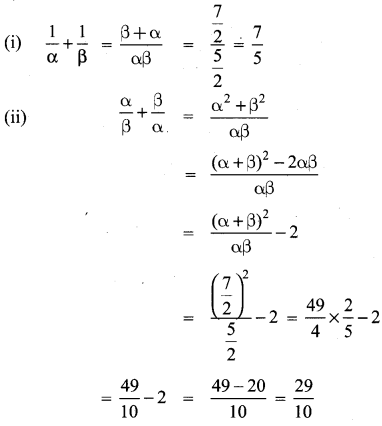
Exercise 3.14 Class 10 Samacheer Question 3.
The roots of the equation x² + 6x – 4 = 0 are α, β. Find the quadratic equation whose roots are
(i) α² and β²
(ii) \(\frac{2}{\alpha} \text { and } \frac{2}{\beta}\)
(iii) α²β and β²α
Solution:
If the roots are given, the quadratic equation is x² – (sum of the roots) x + product the roots = 0.
For the given equation.
x² + 6x – 4 = 0
α + β = -6
αβ = -4
(i) α² + β² = (α + β)² – 2αβ
= (-6)² – 2(-4) = 36 + 8 = 44
α²β² = (αβ)² = (-4)² = 16
∴ The required equation is x² – 44x – 16 = 0.

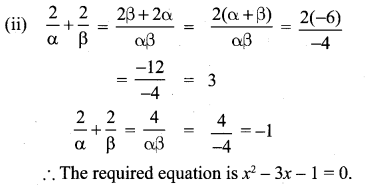
(iii) α²β + β²α = αβ(α + β)
= -4(-6) = 24
α²β × β²α = α³β³ = (αβ)³ = (-4)³ = -64
∴ The required equation = x² – 24x – 64 – 0.

10th Maths Exercise 3.14 Question 4.
If α, β are the roots of 7x² + ax + 2 = 0 and if β – α = \(\frac{-13}{7}\) Find the values of a.
Solution:

10th Maths Exercise 3.14 Solutions Question 5.
If one root of the equation 2y² – ay + 64 = 0 is twice the other then find the values of a.
Solution:
Let one of the root α = 2β
α + β = 2β + β = 3β
Given

a² = 576
a = 24, -24

10th Maths Exercise 3.14 Solution Question 6.
If one root of the equation 3x² + kx + 81 = 0 (having real roots) is the square of the other then find k.
Solution:
3x² + kx + 81 = 0
Let the roots be α and α²