You can Download Samacheer Kalvi 10th Maths Book Solutions Guide Pdf, Tamilnadu State Board help you to revise the complete Syllabus and score more marks in your examinations.
Tamilnadu Samacheer Kalvi 10th Maths Solutions Chapter 1 Relations and Functions Ex 1.6
Question 1.
If n(A × B) = 6 and A = {1, 3} then n(B) is
(1) 1
(2) 2
(3) 3
(4) 6
Answer:
(3) 3
Hint:
If n(A × B) = 6
A = {1, 1}, n(A) = 2
n(B) = 3
Question 2.
A = {a, b,p}, B = {2, 3}, C = {p, q, r, s)
then n[(A ∪ C) × B] is ………….
(1) 8
(2) 20
(3) 12
(4) 16
Answer:
(3) 12
Hint: A ∪ C = [a, b, p] ∪ [p, q, r, s]
= [a, b, p, q, r, s]
n (A ∪ C) = 6
n(B) = 2
∴ n [(A ∪ C)] × B] = 6 × 2 = 12
![]()
Question 3.
If A = {1, 2}, B = {1, 2, 3, 4}, C = {5, 6} and D = {5, 6, 7, 8} then state which of the following statement is true.
(1) (A × C) ⊂ (B × D)
(2) (B × D) ⊂ (A × C)
(3) (A × B) ⊂ (A × D)
(4) (D × A) ⊂ (B × A)
Answer:
(1) (A × C) ⊂ (B × D)]
Hint:
A = {1, 2}, B = {1, 2, 3, 4},
C = {5, 6}, D ={5, 6, 7, 8}
A × C ={(1,5), (1,6), (2, 5), (2, 6)}
B × D = {(1, 5),(1, 6),(1, 7),(1, 8),(2, 5),(2, 6), (2, 7), (2, 8), (3, 5), (3, 6), (3, 7), (3, 8)}
∴ (A × C) ⊂ B × D it is true
Question 4.
If there are 1024 relations from a set A = {1, 2, 3, 4, 5} to a set B, then the number of elements in B is ………………….
(1) 3
(2) 2
(3) 4
(4) 8
Answer:
(2) 2
Hint: n(A) = 5
n(A × B) = 10
(consider 1024 as 10)
n(A) × n(B) = 10
5 × n(B) = 10
n(B) = \(\frac { 10 }{ 5 } \) = 2
n(B) = 2
Question 5.
The range of the relation R = {(x, x2)|x is a prime number less than 13} is
(1) {2, 3, 5, 7}
(2) {2, 3, 5, 7, 11}
(3) {4, 9, 25, 49, 121}
(4) {1, 4, 9, 25, 49, 121}
Answer:
(3) {4, 9, 25, 49, 121}]
Hint:
R = {(x, x2)/x is a prime number < 13}
The squares of 2, 3, 5, 7, 11 are
{4, 9, 25, 49, 121}
![]()
Question 6.
If the ordered pairs (a + 2,4) and (5, 2a + 6) are equal then (a, b) is ………
(1) (2, -2)
(2) (5, 1)
(3) (2, 3)
(4) (3, -2)
Answer:
(4) (3, -2)
Hint:
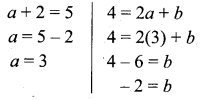
The value of a = 3 and b = -2
Question 7.
Let n(A) = m and n(B) = n then the total number of non-empty relations that can be defined from A to B is
(1) mn
(2) nm
(3) 2mn – 1
(4) 2mn
Answer:
(4) 2mn
Hint:
n(A) = m, n(B) = n
n(A × B) = 2mn
Question 8.
If {(a, 8),(6, b)} represents an identity function, then the value of a and 6 are respectively
(1) (8,6)
(2) (8,8)
(3) (6,8)
(4) (6,6)
Answer:
(1) (8,6)
Hint: f = {{a, 8) (6, 6)}. In an identity function each one is the image of it self.
∴ a = 8, b = 6
Question 9.
Let A = {1, 2, 3, 4} and B = {4, 8, 9, 10}. A function f : A → B given by f = {(1, 4),(2, 8),(3, 9),(4, 10)} is a
(1) Many-one function
(2) Identity function
(3) One-to-one function
(4) Into function
Answer:
(3) One-to one function
Hint:
A = {1, 2, 3, 4), B = {4, 8, 9,10}

Question 10.
If f(x) = 2x2 and g (x) = \(\frac{1}{3 x}\), Then fog is
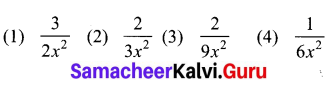
Answer:
(3) \(\frac{2}{9 x^{2}}\)
Hint:
f(x) = 2x2
g(x) = \(\frac{1}{3 x}\)
fog = f(g(x)) = \(f\left(\frac{1}{3 x}\right)=2\left(\frac{1}{3 x}\right)^{2}\)
= 2 × \(\frac{1}{9 x^{2}}=\frac{2}{9 x^{2}}\)
![]()
Queston 11.
If f: A → B is a bijective function and if n(B) = 7 , then n(A) is equal to …………..
(1) 7
(2) 49
(3) 1
(4) 14
Answer:
(1) 7
Hint:
n(B) = 7
Since it is a bijective function, the function is one – one and also it is onto.
n(A) = n(B)
∴ n(A) = 7
Question 12.
Let f and g be two functions given by f = {(0, 1), (2, 0), (3, -4), (4, 2), (5, 7)} g = {(0, 2), (1, 0), (2, 4), (-4, 2), (7, 0)} then the range of fog is
(1) {0, 2, 3, 4, 5}
(2) {-4, 1, 0, 2, 7}
(3) {1, 2, 3, 4, 5}
(4) {0, 1, 2}
Answer:
(4) {0, 1, 2}
Hint:
gof = g(f(x))
fog = f(g(x))
= {(0, 2),(1, 0),(2, 4),(-4, 2),(7, 0)}
Range of fog = {0, 1, 2}
Question 13.
Let f (x) = \(\sqrt{1+x^{2}}\) then ………………..
(1) f(xy) = f(x) f(y)
(2) f(xy) > f(x).f(y)
(3) f(xy) < f(x). f(y)
(4) None of these
Answer:
(3) f(xy) < f(x) . f(y)
![]()
Question 14.
If g = {(1, 1),(2, 3),(3, 5),(4, 7)} is a function given by g(x) = αx + β then the values of α and β are
(1) (-1, 2)
(2) (2, -1)
(3) (-1, -2)
(4) (1, 2)
Answer:
(2) (2,-1)
Hint:
g(x) = αx + β
α = 2
β = -1
g(x) = 2x – 1
g(1) = 2(1) – 1 = 1
g(2) = 2(2) – 1 = 3
g(3) = 2(3) – 1 = 5
g(4) = 2(4) – 1 = 7
Question 15.
f(x) = (x + 1)3 – (x – 1)3 represents a function which is …………….
(1) linear
(2) cubic
(3) reciprocal
(4) quadratic
Answer:
(4) quadratic
Hint: f(x) = (x + 1)3 – (x – 1)3
[using a3 – b3 = (a – b)3 + 3 ab (a – b)]
= (x + 1 – x + 1)3 + 3(x + 1) (x – 1)
(x + 1 – x + 1)
= 8 + 3 (x2 – 1)2
= 8 + 6 (x2 – 1)
= 8 + 6x2 – 6
= 6x2 + 2
It is quadratic polynomial