Samacheer Kalvi 12th Maths Guide Chapter 6 வெக்டர் இயற்கணிதத்தின் பயன்பாடுகள் Ex 6.7

Tamilnadu State Board New Syllabus Samacheer Kalvi 12th Maths Guide Pdf Chapter 6 வெக்டர் இயற்கணிதத்தின் பயன்பாடுகள் Ex 6.7 Textbook Questions and Answers, Notes.

TN Board 12th Maths Solutions Chapter 6 வெக்டர் இயற்கணிதத்தின் பயன்பாடுகள் Ex 6.7

கேள்வி 1.
(2, 3, 6) என்ற புள்ளி வழிச் செல்வதும் \(\frac{x-1}{2}=\frac{y+1}{3}=\frac{z-3}{1}\) மற்றும் \(\frac{x+3}{2}=\frac{y-3}{-5}=\frac{z+1}{-3}\) என்ற கோடுகளுக்கு இணையானதுமான தளத்தின் துணையலகு அல்லாத வெக்டர் சமன்பாடு மற்றும் கார்டீசியன் சமன்பாடுகளைக் காண்க.
தீர்வு:
தளமானது
\(\vec{a}=2 \hat{i}+3 \hat{j}+6 \hat{k}\) புள்ளி வழிச் செல்கிறது மற்றும்
கோடுகள் \(\frac{x-1}{2}=\frac{y+1}{3}=\frac{z-3}{1}\) மற்றும் \(\frac{x+3}{2}\)
= \(\frac{y-3}{-5}=\frac{z+1}{-3}\) க்கு இணையாக இருக்கிறது.
= \(\vec{b}=2 \hat{i}+3 \hat{j}+\hat{k}\) மற்றும் \(\vec{c}=2 \hat{i}-5 \hat{j}-3 \hat{k}\)
\(\vec{b} \times \vec{c}=\left|\begin{array}{ccc}
\hat{i} & \hat{j} & \hat{k} \\
2 & 3 & 1 \\
2 & -5 & -3
\end{array}\right|\)
= \(\hat{i}(-9+5)-\hat{j}(-6-2)+\hat{k}(-10-6)\)
= \(-4 \hat{i}+8 \hat{j}-16 \hat{k}\)
தளத்தின் துணையலகு இல்லாத வெக்டர் சமன்பாடு

கேள்வி 2.
(2, 2, 1), (9, 3, 6) ஆகிய புள்ளிகள் வழிச் செல்லக் கூடியதும் 2x + 6y + 63 = 9 என்ற தளத்திற்குச் செங்குத்தாக அமைவதுமான தளத்தின் துணையலகு வெக்டர் சமன்பாடு மற்றும் கார்டீசியன் சமன்பாடுகளைக் காண்க.
தீர்வு:
கொடுக்கப்பட்ட தளம் புள்ளிகள் \(\vec{a}=2 \hat{i}+2 \hat{j}+\hat{k}\)
மற்றும் \(\vec{b}=9 \hat{i}+3 \hat{j}+6 \hat{k}\) வழிச் செல்கிறது. கொடுக்கப்பட்ட தளத்தின் சமன்பாடு 2x + 6y + 6z = 9. இதை இவ்வாறு எழுதலாம் \(\vec{r} \cdot(2 \hat{i}+6 \hat{j}+6 \hat{k})\) = 9. கொடுக்கப்பட்ட தளம் \(2 \hat{i}+6 \hat{j}+6 \hat{k}\) க்கு செங்குத்து ஆதலால், தேவையான தளம் \(\vec{c}=2 \hat{i}+6 \hat{j}+6 \hat{k}\) -க்கு இணை. ஆகையால் இரண்டு புள்ளி வழிச் செல்லும் மற்றும் வெக்டருக்கு இணையான தளத்தின் வெக்டர் சமன்பாட்டின் துணையலகு வடிவம்

⇒ (x – 2)(6 – 30) – (y – 2)(42 – 10) + (z – 1)(42 – 2) = 0
⇒ (x- 2)(-24) – (y – 2)(32) + (z – 1)(40) = 0
⇒ -24x + 48 – 32y + 64 + 402 – 40 = 0
⇒ -24x – 32y + 40z + 72 = 0
÷ -8 கிடைப்பது,
3x + 4y – 5z – 9 = 0 என்பது கார்டீசியன் வடிவம்.
∴ வெக்டர் சமன்பாட்டின் துணையலகு வடிவம்
\(\vec{r}=\vec{r} \cdot(3 \vec{i}+4 \vec{j}-5 \vec{k})\) = 9.

கேள்வி 3.
(2, 2, 1),(1, -2, 3) என்ற புள்ளிகள் வழிச் செல்வதும் (2, 1,- 3) மற்றும் (-1, 5, -8). என்ற புள்ளிகள் வழிச் செல்லும் நேர்க்கோட்டிற்கு இணையாகவும் அமையும் தளத்தின் துணையலகு வெக்டர் சமன்பாடு, மற்றும் கார்டீசியன் சமன்பாடுகளைக் காண்க..
தீர்வு:
தளம் இரண்டு புள்ளிகள் வழிச் செல்கிறது.
\(\vec{a}=2 \hat{i}+2 \hat{j}+\hat{k}\) மற்றும் \(\vec{b}=\hat{i}-2 \hat{j}+3 \hat{k}\).
(2, 1, -3) மற்றும் (-1, 5, -8) வழிச் செல்லும் நேர்க்கோடு

ஆகையால் தேவையான தளம் வெக்டர் \(\vec{c}=-3 \hat{i}+4 \hat{j}-5 \hat{k}\) க்கு இணை .
இரு புள்ளிகள் \(\vec{a}, \vec{b}\) வழிச் செல்லும் மற்றும் \(\vec{c}\) க்கு இணையான தளத்தின் வெக்டர் சமன்பாட்டின் துணையலகு வடிவம் \(\vec{r}=\vec{a}+s(\vec{b}-\vec{a})+t \vec{c}\),
s, t ∈ ℝ.
\(\vec{r}=2 \hat{i}+2 \hat{j}+\hat{k}+s(-3 \hat{i}-4 \hat{j}+2 \hat{k})\)+ \(t(-3 \hat{i}+4 \hat{j}-5 \hat{k})\), s, t ∈ ℝ
இரண்டு புள்ளி வழிச் செல்லும் மற்றும் வெக்டருக்கு இணையான தளத்தின் கார்டீசியன் வடிவம்
\(\left|\begin{array}{ccc}
x-x_{1} & y-y_{1} & z-z_{1} \\
x_{2}-x_{1} & y_{2}-y_{1} & z_{2}-z_{1} \\
c_{1} & c_{2} & c_{3}
\end{array}\right|=0\)
[∵ (x₁, y₁, z₁) = (2, 2, 1), (x₂, y₂, z₂) = (-1, -2, 3) & (c₁,c₂, c₃) = (-3, 4-5)]
⇒ \(\left|\begin{array}{ccc}
x-2 & y-2 & z-1 \\
-1 & -4 & 2 \\
-3 & 4 & -5
\end{array}\right|=0\)
⇒ (x – 2)(20 – 8) – (y – 2)(5 + 6) + (z – 1)(-4 – 12) = 0
⇒ (x – 2)(12) – (y – 2)(11) + (z – 1)(-16) = 0
⇒ 12x – 24 – 11y + 22 – 16z + 16 = 0
⇒ 12x – 11y – 162 + 14 = 0

கேள்வி 4.
(1,-2,4) என்ற புள்ளி வழிச் செல்வதும் x + 2y – 3z = 11 என்ற தளத்திற்கு செங்குத் தாகவும் \(\frac{x+7}{3}=\frac{y+3}{-1}=\frac{z}{1}\) என்ற கோட்டிற்கு இணையாகவும் அமையும் தளத்தின் துணையலகு அல்லாத வெக்டர் சமன்பாடு மற்றும் கார்டீசியன் சமன்பாடுகளைக் காண்க.
தீர்வு:
\(\vec{a}=\hat{i}-2 \hat{j}+4 \hat{k}\) ……….. (1)
என்ற புள்ளி வழி செல்லும் தளத்தின் சமன்பாடு கொடுக்கப்பட்ட தளத்தின் சமன்பாடு
x + 2y – 3z = 11
⇒ \(\vec{r} \cdot(\hat{i}+2 \hat{j}-3 \hat{k})\) = 11
\(\hat{i}+2 \hat{j}-3 \hat{k}\) என்ற வெக்டருக்கு கொடுக்கப்பட்ட தளம் செங்குத்து
∴ தேவையான தளம் \(\vec{b}=\hat{i}+2 \hat{j}-3 \hat{k}\) ……….. (2)
என்ற வெக்டருக்கு இணை கொடுக்கப்பட்ட தளம் \(\frac{x+7}{3}=\frac{y+3}{-1}=\frac{z}{1}\) என்ற கோட்டிற்கு இணை அதனுடைய 3,-1, 1 திசை விகிதங்கள்
தேவையான தளம் \(\vec{c}=3 \hat{i}-\hat{j}+\hat{k}\) என்ற வெக்டருக்கு இணை …………. (3)
∴ \(\) என்ற புள்ளி வழிச் செல்கிற மற்றும் 6 மற்றும் க்கு இணையான தளத்தின் வெக்டர் சமன்பாட்டின் துணையலகு இல்லாத வடிவம்


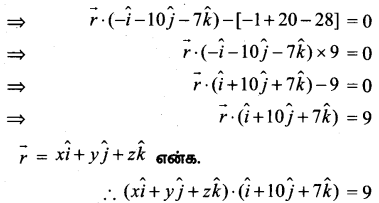
⇒ x + 10y + 7z = 9 என்பது தேவையான தளத்தின் கார்டீசியன் சமன்பாடு ஆகும்.

கேள்வி 5.
\(\vec{r}=(\hat{i}-\hat{j}+3 \hat{k})+t(2 \hat{i}-\hat{j}+4 \hat{k}) .\) என்ற கோட்டை உள்ளடக்கியதும் \(\vec{r} \cdot(\hat{i}+2 \hat{j}+\hat{k})\) = 8 என்ற தளத்திற்குச் செங்குத்தானதுமான தளத்தின் துணையலகு வடிவ வெக்டர் மற்றும் கார்டீசியன் சமன்பாடுகளைக் காண்க.
தீர்வு:
தளம் கொண்டிருக்கும் கோடானது
\(\vec{r}=(\hat{i}-\hat{j}+3 \hat{k})+t(2 \hat{i}-\hat{j}+4 \hat{k}) .\)
∴ தேவைான தளம் \(\vec{a}=\hat{i}-\hat{j}+3 \hat{k}\) என்ற புள்ளி
வழிச் செல்கிறது மற்றும் \(\vec{b}=2 \hat{i}-\hat{j}+4 \hat{k}\) என்ற வெக்டருக்கு இணை.
மேலும், தளம் \(\vec{r} \cdot(\hat{i}+2 \hat{j}+\hat{k})\) என்ற தளத்திற்கு செங்குத்து.
∴ தேவையான தளம் \(\vec{c}=\hat{i}+2 \hat{j}+\hat{k}\) என்ற வெக்டருக்கு இணை
∴ \((\vec{a})\) என்ற புள்ளி வழிச் செல்லும் \(\vec{b}\) மற்றும் \(\vec{c}\) என்ற இரு வெக்டர்களுக்கு இணையான தளத்தின் வெக்டர் சமன்பாட்டின் துணையலகு இல்லாத வடிவம்

⇒ (x – 1)(-1 – 8) – (y + 1)(2 – 4) + (z – 3)(4 + 1) = 0
⇒ (x – 1)(-9) – (y + 1)(-2) + (z – 3)5 = 0
⇒ -9x + 9 +2y + 2 + 5z – 15 = 0
⇒ -9x + 2y + 5z – 4 = 0
⇒ 9x – 2y – 5z + 4 = 0

கேள்வி 6.
(3, 6, -2), (-1, -2, 6), மற்றும் (6, -4, – 2) ஆகிய ஒரே கோட்டிலமையாத மூன்று புள்ளிகள் வழிச் செல்லும் தளத்தின் துணையலகு , துணையலகு அல்லாத வடிவ வெக்டர் மற்றும் கார்டீசியன் சமன்பாடுகளைக் காண்க.
தீர்வு:
\(\vec{a}=3 \hat{i}+6 \hat{j}-2 \hat{k}\)
\(\vec{b}=-\hat{i}-2 \hat{j}+6 \hat{k}\) மற்றும்
\(\vec{c}=6 \hat{i}-4 \hat{j}-2 \hat{k}\)
என்ற மூன்று புள்ளிகள் வழி தளம் செல்கிறது. இங்கு

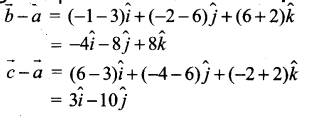
மூன்று புள்ளிகள் வழிச் செல்லும் தளத்தின் வெக்டர் சமன்பாட்டின் துணையலகு வடிவம்

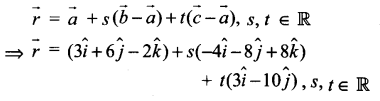
3 புள்ளிகள் வழிச் செல்லும் தளத்தின் வெக்டர் சமன்பாட்டின் துணையலகு இல்லாத வடிவம்

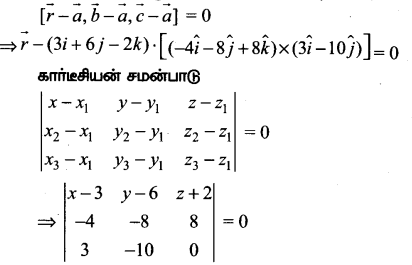
⇒ (x – 3)(0 + 80) – (y – 6)(0 – 24) + (z + 2)(40 + 24) = 0
⇒ 80x – 240 + 24y – 144 + +64z + 128 = 0
⇒ 80x + 24y + 64z – 256 = 0 ÷ 8 கிடைப்பது
10x + 3y + 8z – 32 = 0

கேள்வி 7.
\(\vec{r}=(6 \hat{i}-\hat{j}+\hat{k})+s(-\hat{i}+2 \hat{j}+\hat{k})+t(-5 \hat{i}-4 \hat{j}-5 \hat{k})\) என்ற தளத்தின் துணையலகு அல்லாத வெக்டர் மற்றும் கார்டீசியன் சமன்பாடுகளைக் காண்க.
தீர்வு:
தளத்தின் சமன்பாடு
\(\vec{r}=(6 \hat{i}-\hat{j}+\hat{k})+s(-\hat{i}+2 \hat{j}+\hat{k})+t(-5 \hat{i}-4 \hat{j}-5 \hat{k})\) \(\vec{a}=6 \hat{i}-\hat{j}+\hat{k}\) என்ற புள்ளி வழிச்செல்லும் \(\vec{b}=-\hat{i}+2 \hat{j}+\hat{k}\) மற்றும் \(\vec{c}=-5 \hat{i}-4 \hat{j}-5 \hat{k}\) இணையானது.
∴ தளத்தின் வெக்டர் சமன்பாட்டின் துணையலகு இல்லாத வடிவம் \((\vec{r}-\vec{a}) \cdot(\vec{b} \times \vec{c})=0\)

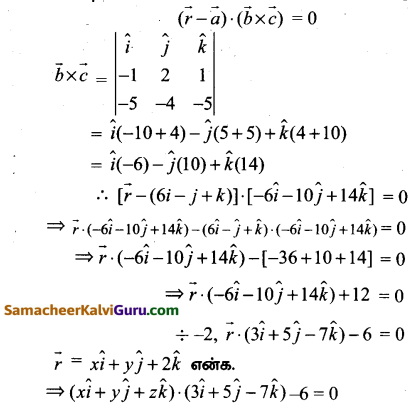
⇒ 3x + 5y – 72 – 6 = 0 என்பது தேவையான கார்டீசியன் சமன்பாடு